支持向量机的直观解释

有两类数据需要分类器进行分类：

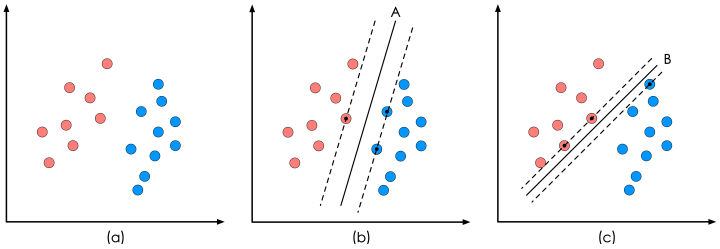
使用感知机可以实现，但是感知机有无数个解，因为感知机只关注样本数据有没有分错，所以无数条直线可以绘制出来，比如A和B

本文我们将使用SVM(support vector machine 支持向量机)来解决它。支持向量机不仅关注样本分类正确性，而且关注测试数据的容错性，简单的说，它会找出唯一的最优直线。或者说最优超平面，什么是最优超平面呢？直观地说，如图中A就是最优分类，它相比B以及其它任何分类面来说，距离两个类别的数据最远，对样本的分类最可信，对测试数据的容纳性最大。

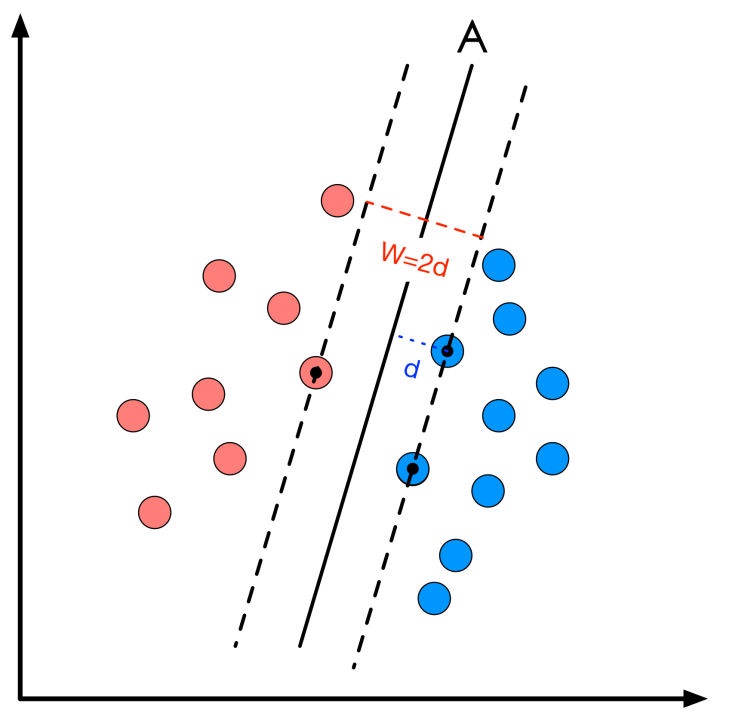
距离两个类别的最近的样本点的距离之和，我们称作“分类间隔”，也就是图中两个虚线之间的距离。最优解对应的两虚线所穿过的样本点，就是SVM中的支持样本点，称为“支持向量”。最优解也就是我们的决策面就是两个虚线之间的中点：

数学推导

超平面计算原理

怎么从众多超平面里面找到最优的哪一个呢？

设我们的数据点为 $(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$ ,其中 $x_i=\begin{bmatrix} x_{i1}\\ x_{i2}\\ ...\\ x_{in} \end{bmatrix}$ 为数据坐标， $y_i$ 为label，我们认为设定取值为-1或1，表示两个类别。

设最优解超平面的数学表示为 $w^{T}x+b=0$ ，其中 $x$ 同上面的数据点，为n维列向量, $w^{T}=(w_1,w_2,...,w_n)$ 为各个维度的参数。

在二维面里，其实展开就是 $w_1x_1+w_2x_2+b=0$ ，当然习惯x-y表示二维坐标的朋友可以看做 $w_1x+w_2y+b=0$

我们找最优超平面就是通过规划条件求解参数 $w,b$

接下来，基于“分类间隔最大”的目标来求超平面，首先我们看看分类间隔如何用 $w,b$ 表示:

由点到面的距离公式并带入label值，我们得到点 $x$ 到超平面的几何距离为：

$d=\frac{|w^Tx+b|}{\|w\|}$

$=y\frac{w^Tx+b}{\|w\|}$

从这个距离里面，我们有两个信息可以挖掘：

1）仅对于支持向量点 $x_s$ 到超平面的几何距离 $\gamma =y_s\frac{w^Tx_s+b}{\|w\|}$ ，我们要尽可能最大化
2）对任何样本点（包括支持向量点） $x_i$ 到超平面的几何距离，要求 $y_i\frac{w^Tx_i+b}{\|w\|}\geq \gamma$

先看1)，我们需要最大化的这个距离包含这么多部分，我们应该改变哪个部分呢？让我们来探索一下：

瞧瞧这一部分： $y_s(w^Tx_s+b)$ ，我们姑且叫它“函数距离”。有没有发现函数距离是可以随意改变的? —— 只要倍数加大 $w,b$ 的值，这时候平面仍是那个平面，因为倍乘之后的超平面 $\lambda w^Tx+\lambda b=0$ 仍然是之前那个平面，但是函数距离变大了！这告诉我们，通过约束我们可以将函数距离固定。这里我们就不妨固定 $y_s(w^Tx_s+b)=1$ 吧！

所以 $\gamma =\frac{1}{\|w\|}$ ，现在我们只需要最小化 $\|w\|$ 就好了。为了之后计算方便（请继续看），我们将该目标转换为：最小化 $\frac{1}{2}\|w\|^2$ 。他们是等价的，这一点我想无须再证明一遍。

再看2)，因为 $\gamma =\frac{1}{\|w\|}$ ，则 $y_i\frac{w^Tx_i+b}{\|w\|}\geq \gamma$ => $y_i(w^Tx_i+b)\geq 1$

综上，我们的问题转换为:

$\underset{w,b}{min} \quad \frac{1}{2}\|w\|^2 \\ s.t.\quad y_i(w^Tx_i+b)\geq 1,\quad i=1,2,...,n$ ①

实例计算

类别一有2个点： $x1=(3,3)^T,\ x2=(4,3)^T$ ，类别二有1个点： $x3=(1,1)^T$ ，求最大间隔分离超平面：

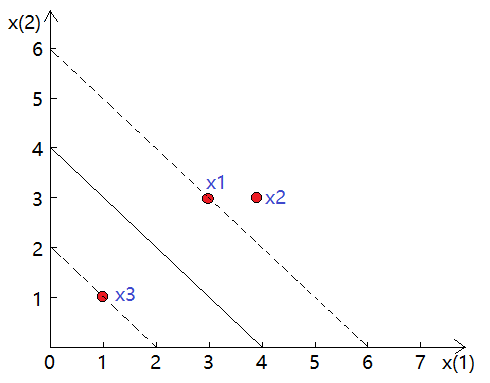
解：

按照上面的约束公式有：

$\underset{w,b}{min}\frac{1}{2}(w_1^2+w_2^2)\\ s.t. \left\{\begin{matrix} 3w_1+3w_2+b\geq 1\\ 4w_1+3w_2+b\geq 1\\ -w_1-w_2-b\geq 1 \end{matrix}\right.$

求得 $w_1=w_2=\frac{1}{2},\ b=-2$ ，所以最大间隔分离超平面为：

$\frac{1}{2}x^{(1)}+\frac{1}{2}x^{(2)}-2=0$

其中 $x1,x3$ 为支持向量

对偶算法推导

上面的例子样本点太少，所以可以方便地计算，那么在大量数据的条件下，我们改怎么办？接下来的会通过这个路径解释:

拉格朗日乘子法->KKT条件->对偶算法

拉格朗日乘子法

当我们遇到含有等式约束的优化问题，可以借助拉格朗日乘子法。也就是说在 $g(x)=0$ 条件下求 $f(x)$ 的最小或最大值，可以通过构造 $L(x,\lambda)=f(x)+\lambda g(x)$ ，然后让它分别对 $x,\lambda$ 的偏导数为0来求解极值。

KKT条件

而当约束含有是不等式的时候，我们需要在拉格朗日乘子法基础上构建KKT条件来帮助求解。这里我们要求的超平面问题就是此类问题。
为了方便说明我们考虑只有一个小于不等式约束求极小值的情况，因为即使是大于（极大值），也可以用两边取负数来变成小于（极小值），即使有很多个不等式，也可以通过加权表示。问题表述为：在 $g(x)\leq 0$ 约束下求 $f(x)$ 的极小值：

$min\ f(x)\\ s.t.\ g(x)\leq 0$ ②

画出图如下：

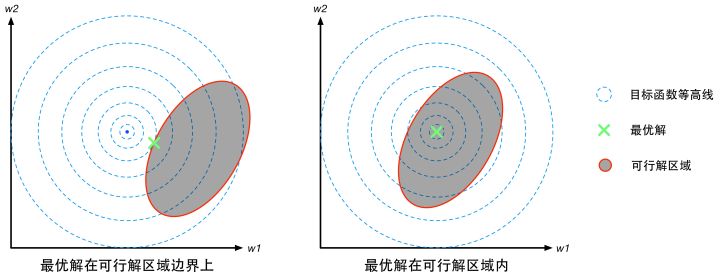
它的解：a）要么在边界上，也就是不等式变成等式，b）要么在可行解区域。

a）当解在边界上时，就是拉格朗日乘子法 $L(x,\lambda)=f(x)+\lambda g(x)$ ，但是它相比拉格朗日乘子法还多了一个信息，即排除了可行解区域，也就是说排除了 $g(x)< 0$ 的情况。也就是说越往椭圆的外面走，目标函数 $f(x)$ 值越小，越接近极小值，走到边界的时候取到了约束条件下的最小值，而相反的是 $g(x)$ 越往椭圆外走值越大，所以 $f(x)$ 与 $g(x)$ 在这个方向上的导数正负相反。又因为取最优解时，偏导数为0： $\frac{\partial L(x,\lambda)}{\partial x}=\frac{\partial f(x)}{\partial x}+\lambda \frac{\partial g(x)}{\partial x}=0$ ，所以 $\lambda >0$

b）当解在可行解区域里时，相当于约束条件不起作用，也就是 $L(x,\lambda)=f(x)+\lambda g(x)$ 里面的 $\lambda =0$ ，只是在最后如果求得的极值有多个的时候，要取满足 $g(x)<0$ 的那一个

集合a)和b)两种情况，我们可以写出一个统一的表达：

$min\ L(x,\lambda)=f(x)+\lambda g(x) \\ s.t. \left\{\begin{matrix} g(x)\leq 0 \\ \lambda\geq 0\\ \lambda g(x)=0 \end{matrix}\right.$ ③

以上约束条件就是KKT条件

到这，可能有人说，怎么条件看起来更复杂了？其实是因为这样对之后对偶算法推导是非常方便的，并且注意，之前的约束是对于可行解区域而言，现在的约束条件是针对最优解的，因为它包含了解是在边界还是在可行解区域的信息。

拉格朗日对偶

拉格朗日求解最优化的思想本来就是把约束条件整合到新的目标函数 $L(x,\lambda)$ 里面去，从而消去了约束条件，但是上节的操作虽然生成了 $L(x,\lambda)$ ，但是约束条件不仅没有消去，还产生了包含更多条件的KKT。别着急，我们推导出KKT条件的努力不会白费，先放着它，之后会用到。

准备：新目标函数

接下来，我们重新从问题的源头开始，去整合出一个不含约束条件的新的目标函数。考虑通用性，我们把问题的源头扩展到更通用的表述，即我们有多个等式约束和多个不等式约束同时存在：

$min\ f(x)\\ s.t.\ \ \left\{\begin{matrix} h_i(x)=0\ \ i=1,2,...,m \\g_j(x)\leq 0\ \ j=1,2,...,n \end{matrix}\right.$ ④

因为这里我们求的是最小值，所以我们想象一个这样的新的目标函数：它在本身在约束条件之外的取值是无穷大的，而在约束条件内的取值是和 $f(x)$ 一样的。如果我们能找到这样一个新的目标函数，就不需要约束条件了。

我们考虑下面的新目标函数：

$\theta_P(x)=\underset{\alpha,\beta;\beta_j\geq 0}{max\ L(x,\alpha,\beta)}$

其中 $L(x,\alpha,\beta)$ 为广义拉格朗日函数

$L(x,\alpha,\beta)=f(x)+\sum_{i=1}^{m}\alpha _ih_i(x)+\sum_{j=1}^{n}\beta _jg_j(x)$

上面的式子注意两点：1） $\beta_j\geq 0$ 已经在上面的 $\lambda\geq 0$ 得到证明了； 2） $\underset{\alpha,\beta;\beta_j\geq 0}{max\ L(x,\alpha,\beta)}$ 是只关于 $\alpha,\beta$ 的函数， $x$ 在这里看做常量

继续推导出：

$\theta_P(x)=\underset{\alpha,\beta;\beta_j\geq 0}{max\ L(x,\alpha,\beta)}=\underset{\alpha,\beta;\beta_j\geq 0}{max}[f(x)+\sum_{i=1}^{m}\alpha_ih_i(x)+\sum_{j=1}^{n}\beta_jg_j(x)]$ ⑤

顺便说一下，因为 $f(x)$ 与 $\alpha,\beta$ 无关，所以：⑤= $f(x)+\underset{\alpha,\beta;\beta_j\geq 0}{max}[\sum_{i=1}^{m}\alpha_ih_i(x)+\sum_{j=1}^{n}\beta_jg_j(x)]$ ，这个条件待会会用到

参照④中的约束条件，我们对⑤式的解进行分析：

1）在约束条件内，即当 $h_i(x)=0,g_j(x)\leq 0$ 时， $\underset{\alpha,\beta;\beta_j\geq 0}{max}[\sum_{i=1}^{m}\alpha_ih_i(x)+\sum_{j=1}^{n}\beta_jg_j(x)]=0$

2）在约束条件外，即 $h_i(x)=0,g_j(x)\leq 0$ 两个条件中至少有一个不满足。如果 $h_i(x)\neq 0$ 则通过合理取值，可以得到： $\underset{\alpha,\beta;\beta_j\geq 0}{max}[\sum_{i=1}^{m}\alpha_ih_i(x)+\sum_{j=1}^{n}\beta_jg_j(x)]=+\infty$ ；如果 $g_j(x)>0$ ，则通过合理取值，也可以得到： $\underset{\alpha,\beta;\beta_j\geq 0}{max}[\sum_{i=1}^{m}\alpha_ih_i(x)+\sum_{j=1}^{n}\beta_jg_j(x)]=+\infty$

结合上面两种情况(设约束条件集合为 $\Phi$ )：

$\theta_P(x)=\left\{\begin{matrix} f(x),\ x\epsilon \Phi \\ +\infty ,\ otherwise \end{matrix}\right.$

所以没错，我们要找的新目标函数就是 $\theta_P(x)$ ，那么我们的问题转换为：

$\min_{x}\ \theta_P(x)= \min_{x}[\max_{\alpha,\beta;\beta_j\geq0}L(x,\alpha,\beta) ]$ ⑥

此时，如果去计算 $\theta_P(x)$ 的极小值，不管通过导数为0还是梯度下降，都会发现 $\alpha,\beta$ 这两个参数没法去掉。怎么办？虽然我们消去了约束条件，找到了新的目标函数，但是似乎我们引入的 $\alpha,\beta$ 变成了新的屏障？

为了解决这个问题，我们的对偶算法终于要登场了！

对偶同解的引入

我们构造一个与 $\theta_P(x)$ 类似的函数： $\theta_D(\alpha,\beta)=\min_{x}L(x,\alpha,\beta)$ ，然后定义一个最大值问题：

$\underset{\alpha,\beta;\beta\geq 0}{max}\ \theta_D(\alpha,\beta)= \underset{\alpha,\beta;\beta\geq 0}{max}\ [\min_{x}\ L(x,\alpha,\beta)]$ ⑦

对比⑦和⑥，发现它们无论从函数还是参数限制上，都具有一种对称性。注意这里的变量是 $\alpha,\beta$ ，而⑥的变量是 $x$ ，他们达到的极值不一样，要求的最优解也不一样

然后呢，这种对称有什么用？我直接给出结论好了：

结论一： ⑦和⑥互为对偶问题，且在最值关系上有⑦<⑥。

结论二：在结论一的基础上，如果满足KKT（终于派上用场了！）条件，则⑦和⑥互为强对偶关系，两者等价。也就是说可以用求解⑦来替代求解⑥

下面我们总结一下问题的求解流程

通用对偶化求解流程

假设要求一个问题： $min\ f(x)\\ s.t.\ \ \left\{\begin{matrix} h_i(x)=0\ \ i=1,2,...,m \\g_j(x)\leq 0\ \ j=1,2,...,n \end{matrix}\right.$

流程是——

消去约束条件，转换为等价的新目标函数： $\min_{x}\ \theta_P(x)= \min_{x}\ \max_{\alpha,\beta;\beta_j\geq0}[f(x)+\sum_{i=1}^{m}\alpha _ih_i(x)+\sum_{j=1}^{n}\beta _jg_j(x)]$

↓

转换为对偶问题： $\underset{\alpha,\beta;\beta\geq 0}{max}\ \theta_D(\alpha,\beta)= \underset{\alpha,\beta;\beta\geq 0}{max}\ \min_{x}\ [f(x)+\sum_{i=1}^{m}\alpha _ih_i(x)+\sum_{j=1}^{n}\beta _jg_j(x)]$

↓

确定最原始的问题满足KKT条件

↓

求对偶问题的最优解，即为原始问题的最优解

最优超平面求解问题的对偶化

利用上面的流程，我们来试一试求解SVM里面最优超平面问题。

我们的问题是：

$\underset{w,b}{min} \quad \frac{1}{2}\|w\|^2 \\ s.t.\quad y_i(w^Tx_i+b)\geq 1,\quad i=1,2,...,n$

解：
首先明确我们问题中的各个部分：
$f(w,b)=\frac{1}{2}\|w\|^2$

$h_i(w,b)=0$

$g_j(w,b)=1-y_j(w^Tx_j+b),\ \ j=1,2,...,n$

1）消去约束条件，得到： $\min_{w,b}\ \theta_P(x)= \min_{w,b}\ \max_{\beta;\beta_j\geq0}\{\frac{1}{2}\|w\|^2+\sum_{j=1}^{n}\beta _j[1-y_i(w^Tx_i+b)]\}$

2）转换为对偶问题： $\underset{\beta;\beta\geq 0}{max}\ \theta_D(\beta)= \underset{\beta;\beta\geq 0}{max}\ \min_{w,b}\ \{\frac{1}{2}\|w\|^2+\sum_{j=1}^{n}\beta _j[1-y_i(w^Tx_i+b)]\}$ ⑧

3）再看是否满足KKT的条件。——满足

4）求对偶问题⑧的解。

这个实例里， $L(w,b,\beta)=\frac{1}{2}\|w\|^2+\sum_{j=1}^{n}\beta _j[1-y_i(w^Tx_i+b)]$

求偏导数为0：

$\frac{\partial L(w,b,\beta) }{\partial w }=w-\sum_{j=1}^{n}\beta_jy_jx_j=0$ => $w=\sum_{j=1}^{n}\beta_jy_jx_j$ ⑨

$\frac{\partial L(w,b,\beta) }{\partial b }=-\sum_{j=1}^{n}\beta_jy_j=0$ => $\sum_{j=1}^{n}\beta_jy_j=0$ ⑩

把⑨带入到 $L(w,b,\beta)$ 中，并利用⑩，得：

$L(w,b,\beta)=-\frac{1}{2}\sum_{j=1}^{n}\sum_{k=1}^{n}\beta_j\beta_ky_jy_k(x_jx_k)+\sum_{j=1}^{n}\beta_j$

因为它与 $w,b$ 无关了，所以：

$\theta_D(\beta)=\underset{w,b}{min }\ L(w,b,\beta)=-\frac{1}{2}\sum_{j=1}^{n}\sum_{k=1}^{n}\beta_j\beta_ky_jy_k(x_jx_k)+\sum_{j=1}^{n}\beta_j$

$\underset{\beta;\beta\geq 0}{max}\ \theta_D(\beta)= \underset{\beta;\beta\geq 0}{max}\ [-\frac{1}{2}\sum_{j=1}^{n}\sum_{k=1}^{n}\beta_j\beta_ky_jy_k(x_jx_k)+\sum_{j=1}^{n}\beta_j]=$

$= \underset{\beta;\beta\geq 0}{min}\ [\frac{1}{2}\sum_{j=1}^{n}\sum_{k=1}^{n}\beta_j\beta_ky_jy_k(x_jx_k)-\sum_{j=1}^{n}\beta_j]$

我们把表达式里面的 $\beta_j\geq 0$ 单独抽离出来，再加上⑩，我们把问题转换为：

$\underset{\beta}{min}\ [\frac{1}{2}\sum_{j=1}^{n}\sum_{k=1}^{n}\beta_j\beta_ky_jy_k(x_jx_k)-\sum_{j=1}^{n}\beta_j] \\ s.t.\ \ \left\{\begin{matrix} \sum_{j=1}^{n}\beta_jy_j=0\\ \beta_j\geq 0,\ \ j=1,2,...,n \end{matrix}\right.$

处于跟上面推导保持一致的原因，这里我使用的变量是 $j,k,\beta$ ，现在一切都推导完了，让我换回到熟悉的 $i,j,\alpha$ :

${\color{Red}\underset{\alpha}{min}\ [\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum_{i=1}^{n}\alpha_i] }\\ {\color{Red}s.t.\ \ \left\{\begin{matrix} \sum_{i=1}^{n}\alpha_iy_i=0\\ \alpha_i\geq 0,\ \ i=1,2,...,n \end{matrix}\right.}$ ⑪

到这里，我们的问题应该方便求解多了。记得，最大间隔超平面认准式⑪！

针对上式，我们多说一句，当 $x_i$ 为非支持向量的点时，对应的 $\alpha$ ，从直观上理解：因为SVM的分类超平面只与支持向量相关。

接下来，求 $w$ ：根据式⑨可以求得

求 $b$ ：通过原始的 $y_i(w^Tx_i+b)\geq 1,\quad i=1,2,...,n$ 建立n个不等式，可以求得b。

不过最方便的是通过这个公式求： $b=-\frac{min_{y_i=1}\ w^Tx_i + max_{y_i=-1}\ w^Tx_i}{2}$ ，该公式推导如下：

所有正向类到超平面的几何距离都大于等于1，其中距离超平面最近的那个等于1： $min_{y_i=1}\ (w^Tx_i+b)=1$

所有负向类到超平面的几何距离都小于等于-1，其中距离超平面最近的那个等于-1： $max_{y_i=-1}\ (w^Tx_i+b)=-1$

联合两个式子，得到：

$min_{y_i=1}\ (w^Tx_i+b)+max_{y_i=-1}\ (w^Tx_i+b)=0$

$min_{y_i=1}\ w^Tx_i++max_{y_i=-1}\ w^Tx_i=-2b$

$b=-\frac{min_{y_i=1}\ w^Tx_i + max_{y_i=-1}\ w^Tx_i}{2}$

超平面对偶算法里的KKT条件

在上面的求解超平面的算法中，KKT条件表现更具体更有几何意义：

1） $\alpha_i$ 在约束条件的边界上，即 $\alpha_i=0$ 时， $y_i(w^Tx_i+b)>1$ ，这意味着非支持向量的系数 $\alpha_i$ 为0，分类器跟非支持向量无关。

2） $\alpha_i$ 在约束条件的非边界上，即 $\alpha_i>0$ 时， $y_i(w^Tx_i+b)=1$ ，这意味着分类器跟支持向量有关。

求解试验

依旧计算一下上面“实例计算”里的例子。

将例子里给的数据，带入到式⑪中：

⑪= $\underset{\alpha}{min}\ \frac{1}{2}(18\alpha_1^2+25\alpha_2^2+2\alpha_3^2+42\alpha_1\alpha_2-12\alpha_1\alpha_3-14\alpha_2\alpha_3)-\alpha_1-\alpha_2-\alpha_3 \\ s.t. \left\{\begin{matrix} \alpha_1+\alpha_2-\alpha_3=0\\ \ \alpha_i\geq 0,\ \ i=1,2,3 \end{matrix}\right.$

解：

将 $\alpha_3=\alpha_1+\alpha_2$ 代入目标函数，则问题转化为:

$\underset{\alpha}{min}\ 4\alpha_1^2+\frac{13}{2}\alpha_2^2+10\alpha_1\alpha_2-2\alpha_1-2\alpha_2\\s.t. \ \ \alpha_i\geq 0,\ \ i=1,2,3$

求解以上问题：

设 $\theta_D(\alpha_1,\alpha_2)=4\alpha_1^2+\frac{13}{2}\alpha_2^2+10\alpha_1\alpha_2-2\alpha_1-2\alpha_2$

求偏导数为0，可以得到在 $\alpha_1=\frac{3}{2},\alpha_2=-1$ 取极值，但是这个不满足约束条件 $\alpha_i\geq 0$ ，所以最优解应该在边界上（也就是至少有一个 $\alpha_i= 0$ ）取。

容易求得当 $\alpha_1= \frac{1}{4}，\alpha_2=0,\alpha_3=\frac{1}{4}$ 时达到最小。进而：

求得 $w_1=w_2=\frac{1}{2},\ b=-2$ ，所以最大间隔分离超平面为：

$\frac{1}{2}x^{(1)}+\frac{1}{2}x^{(2)}-2=0$

其中 $x1,x3$ 为支持向量

线性不可分：软间隔最大化

上面所有讲的情况，是针对线性可分的情况，也就是说一定能找到一个超平面，实现百分之百准确地将样本数据分类。我们训练一个SVM分类器，是为了实际应用，而实际中并不是所有样本都是线性可分的，应该允许在线性不可分的情况下训练SVM分类器，即使有一些数据被误分了。

回顾一下线性可分的SVM问题描述：

$\underset{w,b}{min} \quad \frac{1}{2}\|w\|^2 \\ s.t.\quad y_i(w^Tx_i+b)\geq 1,\quad i=1,2,...,n$

我们期望改装它来兼容线性不可分的情况。

在线性不可分的时候，被误分的数据不能满足间隔条件： $y_i(w^Tx+b)\geq 1$ ，此时，我们给这些点一个大于0的松弛变量 $\xi _i$ 让它能够满足： $y_i(w^Tx+b)\geq 1-\xi_i$

同时，我们对目标函数投入一个惩罚，变成： $\frac{1}{2}\|w\|^2+C\sum_{i=1}^{n}\xi_i$ ,其中C为惩罚参数，是根据实际问题确定的。C体现着对误分率的容忍程度，当C很大的时候，惩罚更严重，因为目标函数更难最小化。

总之现在的问题转换成了含有惩罚项以及两个不等式约束条件的问题：

$\underset{w,b,\xi}{min} \ \ \frac{1}{2}\|w\|^2+C\sum_{i=1}^{n}\xi_i\\ s.t. \left\{\begin{matrix} \ \ y_i(w^Tx_i+b)\geq 1-\xi_i,\ \ i=1,2,...,n\\ \xi_i\geq 0,\ \ i=1,2,...,n \end{matrix}\right.$ ⑫

它的拉格朗日表达式为:

$L(w,b,\alpha,\mu)=\frac{1}{2}\|w\|^2+C\sum_{i=1}^{n}\xi _i+\sum_{i=1}^{n}\alpha_i[1-\xi _i-y_i(w^Tx_i+b)]+(-\sum_{i=1}^{n}\mu_i\xi _i )$

接着，经过一系列操作（详情参考上面的推导），我们获得了原始问题⑫的对偶问题：

${\color{Red}\underset{\alpha}{min}\ \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum_{i=1}^{n}\alpha_i}\\ {\color{Red}s.t.\ \ \left\{\begin{matrix} \sum_{i=1}^{n}\alpha_iy_i=0\\ 0\leq \alpha_i\leq C,\ \ i=1,2,...,n \end{matrix}\right.}$ ⑬

线性不可分的最大软间隔超平面，认准式⑬！

软间隔最大化里的KKT条件

考虑到软间隔最大化的分类器求解才是真正具有通用性的，我们来看这时候的KKT条件：

1） $\alpha_i$ 在约束条件的左边界上，即 $\alpha_i=0$ 时， $w^Tx_i+b>1$ ，这意味着该点 $x_i$ 是正类别且非支持向量。

2） $\alpha_i$ 在约束条件的右边界上，即 $\alpha_i=C$ 时， $w^Tx_i+b<-1$ ，这意味着该点 $x_i$ 是负类别且非支持向量。

3） $\alpha_i$ 在约束条件的非边界上，即 $0<\alpha_i<C$ 时， $y_i(w^Tx_i+b)=1$ ，这意味着该点是支持向量。

核技巧

准备工作

我们知道SVM的分类决策函数是

$f(x)=w^Tx+b$ ，将⑨式的 $w=\sum_{j=1}^{n}\beta_jy_jx_j$ 代入其中，得到：

$f(x)=(\sum_{j=1}^{n}\beta_jy_jx_j)^Tx+b \\ =\sum_{j=1}^{n}[\beta_jy_j(x_j^Tx)]+b \\ =\sum_{j=1}^{n}[\beta_jy_j<x_j,x>]+b$

其中<>表示两个向量的内积。又我们知道最大间隔超平面只跟支持向量有关，所以所有非支持向量样本点的 $\beta_j=0$ ，那么上式子就意味着，一个新的点 $x$ 的分类结果，来自于它跟支持向量点们的内积加权和。

这个结论对于接下来的要讲的核函数有着基础的意义

核函数

在线性不可分的情况下，比如下图左，可以有非线性函数作为分割面，但是这样非常不利于我们求解。于是想到，如下图右，通过升维的方式将图形在新的空间表示，原来的非线性函数经过这次升维就变成了线性超平面。

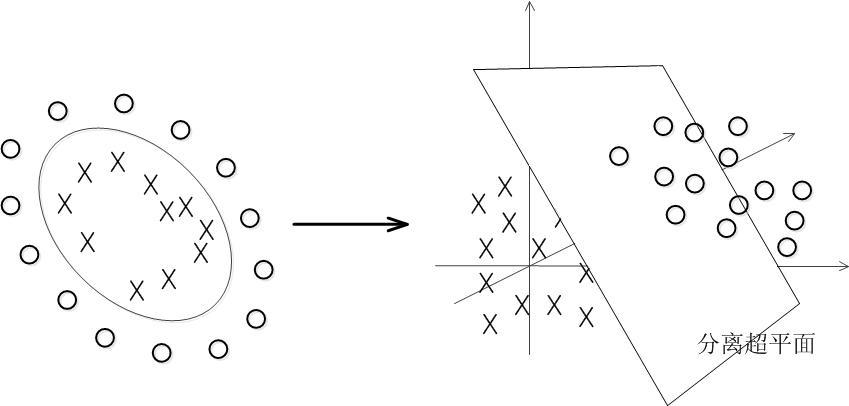
现在的难点在于，我们怎么去升维。

最笨的方法是强行将非线性表达式整合为线性：比如非线性分类面为 $a_1x_1^2+a_2x_2^2+a_3x_1x_2+a_4x_1+a_5x_2+a_6$ ，那么令 $z_1=x_1^2,z_2=x_2^2,z_3=x_1x_2,z_4=x_1,z_5=x_2$ ，就转换成了 $a_1z_1+a_2z_2+a_3z_3+a_4z_4+a_5z_5+a_6$ ，所以二维升到五维之后变成了线性。

我们看到升维操作会导致维度急剧上升，它会导致：当有一个新的数据需要被分类的时候，它需要跟所有支持向量点进行内积，而维度越多，每次内积消耗的计算成本就越大。于是我们希望有一种转换，让我们算升维后的内积更轻松一点，就像算升维之前的内积一样。

核函数的定义

我们考虑这个映射：

$\phi ((x,y))=(x^2,\sqrt{2}xy,y^2)$

它把二维空间升维到三维了。把二维坐标点 $(x,y)$ 变换成了三维的 $(x^2,\sqrt{2}xy,y^2)$ ，比如把 $(1,2)$ 变换到新空间的 $(1,2\sqrt{2},4)$

有两个向量 $(a,b),(c,d)$ 在升维后进行内积操作：

$<\phi ((a,b)),\phi ((c,d))> =\ <(a^2,\sqrt{2}ab,b^2),(c^2,\sqrt{2}cd,d^2)>\\ =\ a^2c^2+2abcd+b^2d^2\\ =\ (<(a,b),(c,d)>)^2$

可以看到，升维后三维的内积可以用升维前二维的内积再平方表示。当然这里是针对这个映射而言。推广到通常地，升维后的内积总是可以转换为升维前的内积的函数，从而避免了直接计算大维度的内积，我们把这个转换叫做核函数，核函数的函数值就是升维后的内积。比如上面例子的核函数是： $k(X_1,X_2)=<\Phi(X_1),\Phi(X_2)>=(<X_1,X_2>)^2$

用核技巧分类

上面推导过，任何线性可分的样本集都可以通过式⑬来找到它的SVM分类超平面（将内积写成<>的格式）:

$\underset{\alpha}{min}\ \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j<x_i,x_j>-\sum_{i=1}^{n}\alpha_i\\ s.t.\ \ \left\{\begin{matrix} \sum_{i=1}^{n}\alpha_iy_i=0\\ 0\leq \alpha_i\leq C,\ \ i=1,2,...,n \end{matrix}\right.$

其中 $x_i,x_j$ 当然是该线性可分数据集里的数据，在现在讲的状况里，就是升维后的数据坐标。

设升维前的数据点是 $X_i,X_j$ ，升维的映射函数是 $\phi$ ，则升维后的分类器可以通过下面得到：

$\underset{\alpha}{min}\ \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j<\phi(X_i),\phi(X_j)>-\sum_{i=1}^{n}\alpha_i\\ s.t.\ \ \left\{\begin{matrix} \sum_{i=1}^{n}\alpha_iy_i=0\\ 0\leq \alpha_i\leq C,\ \ i=1,2,...,n \end{matrix}\right.$

将核函数 $k(X_i,X_j)=<\Phi(X_i),\Phi(X_j)>$ 代入上式，则上式变为：

$\underset{\alpha}{min}\ \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_j{\color{Red}k(X_i,X_j)}-\sum_{i=1}^{n}\alpha_i\\ s.t.\ \ \left\{\begin{matrix} \sum_{i=1}^{n}\alpha_iy_i=0\\ 0\leq \alpha_i\leq C,\ \ i=1,2,...,n \end{matrix}\right.$ ⑭

然后开始求各个参数并得到分类器：

1）通过上式可以求得 $\alpha_i$ ，接下来因为不知道映射 $\phi$ 是什么，所以我们无法通过 $w=\sum_{i=1}^{n}\alpha_iy_i\phi(X_i)$ 来求 $w$ ，但是没关系，因为我们可以把它消掉转而用核函数来表示。

2）先求b:

$b=-\frac{min_{y_i=1}\ w^T\phi(X_i)+max_{y_i=-1}\ w^T\phi(X_i)}{2}\\ =-\frac{min_{y_i=1}\ (\sum_{j=1}^{n}\alpha_jy_j\phi(X_j))^T\phi(X_i)+max_{y_i=-1}\ (\sum_{j=1}^{n}\alpha_jy_j\phi(X_j))^T\phi(X_i)}{2}\\ =-\frac{min_{y_i=1}\ \sum_{j=1}^{n}(\alpha_jy_j<\phi(X_j)),\phi(X_i)>)+max_{y_i=-1}\ \sum_{j=1}^{n}(\alpha_jy_j<\phi(X_j)),\phi(X_i)>)}{2}\\ =-\frac{min_{y_i=1}\ \sum_{j=1}^{n}[\alpha_jy_j{\color{Red}k(X_j,X_i)}]+max_{y_i=-1}\ \sum_{j=1}^{n}[\alpha_jy_j{\color{Red}k(X_j,X_i)}]}{2}$

3）再求分类器：

目标分类器为 $f(x)=w^T\phi(X)+b$ ，将 $w=\sum_{i=1}^{n}\alpha_iy_i\phi(X_i)$ 代入其中，得到：

$f(x)=[\sum_{i=1}^{n}\alpha_iy_i\phi(X_i)]^T\phi(X)+b \\ =\sum_{i=1}^{n}[\alpha_iy_i(\phi(X_i)^T\phi(X))]+b \\ =\sum_{i=1}^{n}[\alpha_iy_i<\phi(X_i),\phi(X)>]+b\\ =\sum_{i=1}^{n}[\alpha_iy_i{\color{Red}k(X_i,X)}]+b$

求解完毕。

常用核函数

现实中做工程，我们能拿到标注好label的数据集就很不错了，更别说核函数了。没有核函数怎么训练一个SVM分类器？——“猜”一个核函数

并不是所有函数都可以作为核函数，只有满足Mercer’s condition（自行Google or Bing）的函数才能成为核函数。根据不同功能，我们有一些常用的核函数有：多项式核函数，高斯核函数，字符串核函数等。

常用核函数部分，不作详细介绍，请自行Google or Bing

SMO算法

目标：求解⑭里的 $(\alpha_1,\alpha_2,..,\alpha_n)$

但是求出所有n个 $\alpha$ : $(\alpha_1,\alpha_2,..,\alpha_n)$ 并不是那么容易的，为此提出了SMO（Sequential Minimal Optimization）算法。

首先选择两个变量 $\alpha_1,\alpha_2$ ，把其它变量 $(\alpha_3,\alpha_4,..,\alpha_n)$ 固定当做常量，于是问题简化为只与 $\alpha_1,\alpha_2$ 有关：

$\underset{\alpha_1,\alpha_2}{min}\ W(\alpha_1,\alpha_2)=\frac{1}{2}K_{11}\alpha_1^2+\frac{1}{2}K_{22}\alpha_2^2+y_1y_2K_{12}\alpha_1\alpha_2-(\alpha_1+\alpha_2)+y_1\alpha_1\sum_{i=3}^{n}y_i\alpha_iK_{i1}+y_2\alpha_2\sum_{i=3}^{n}y_i\alpha_iK_{i2}\\ s.t.\ \ \left\{\begin{matrix} \alpha_1y_1+\alpha_2y_2=-\sum_{i=3}^{n}y_i\alpha_i=\zeta \\ 0\leq \alpha_i\leq C,\ \ i=1,2 \end{matrix}\right.$

其中 $\zeta$ 是出于方便设的常数量表示，而 $K_{ij}$ 是核函数 $k(x_i,x_j)$ 的人为简写

上面是一个二元（ $\alpha_1,\alpha_2$ ）二次规划问题，非常常见。

怎么求这个二次规划问题呢。发现约束条件里面 $\alpha_1,\alpha_2$ 有线性关系，将 $\alpha_2$ 用 $\alpha_1$ 表示代入目标函数，则问题变成了一元二次规划问题。这里注意 $\alpha_1,\alpha_2$ 的线性关系有几种不同情况，我们可以假设 $y_1=y_2=1$ ，如果没有符合条件的解，可以再切换别的假设。