感知机模型
在n维度空间,有m个数据组成的线性可分的数据集,每个数据点都有对应的类别
,但一共只有两个类别:
,则存在一个超平面
,( 其中
)能够准确地将所有的C1和C2数据区分开来,使得他们分别在在超平面的两边。
感知机只针对线性可分的数据,超平面在二维空间是一条线,在三维空间就是一个平面。
线性可分: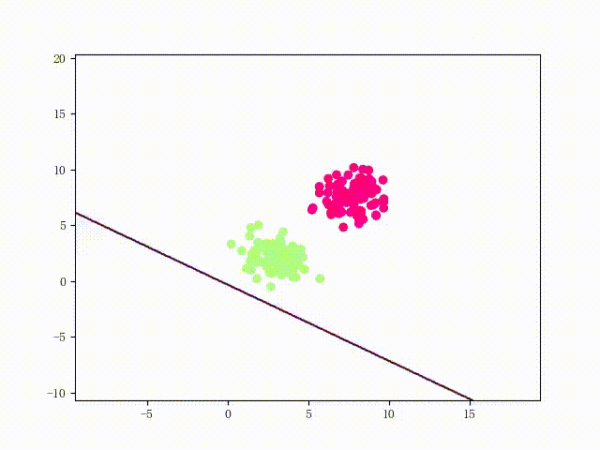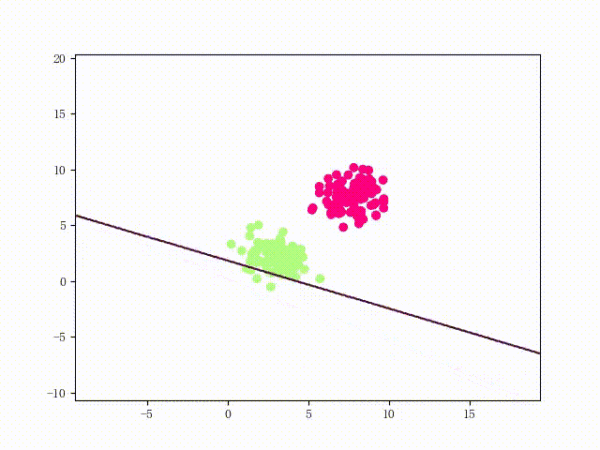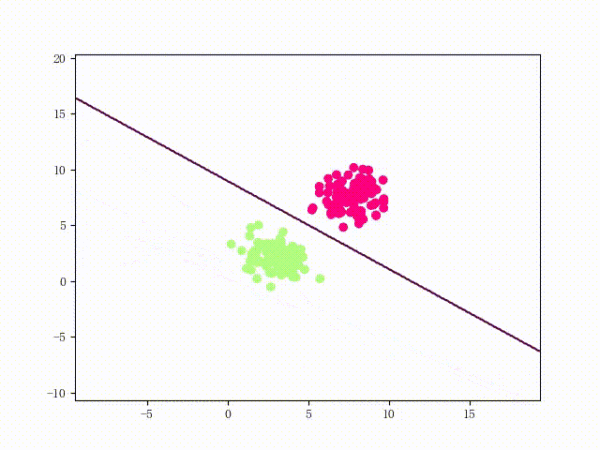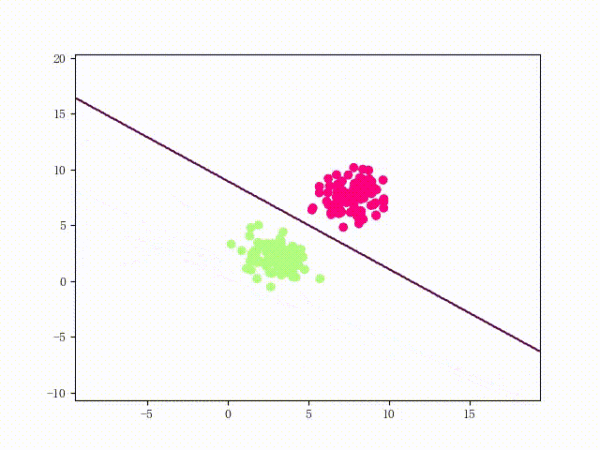
线性不可分: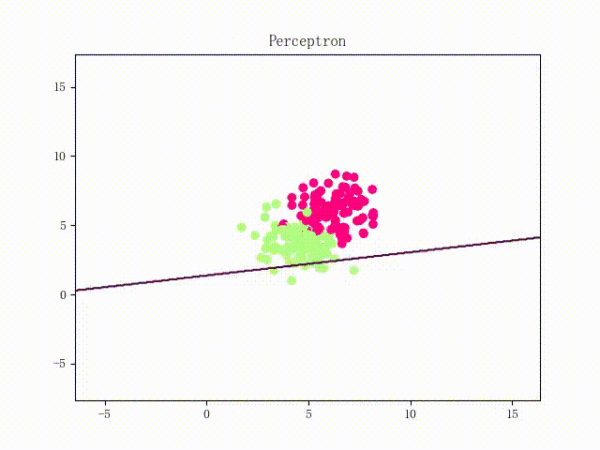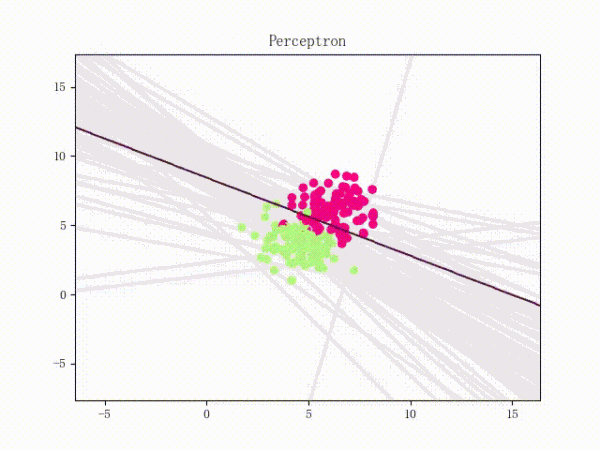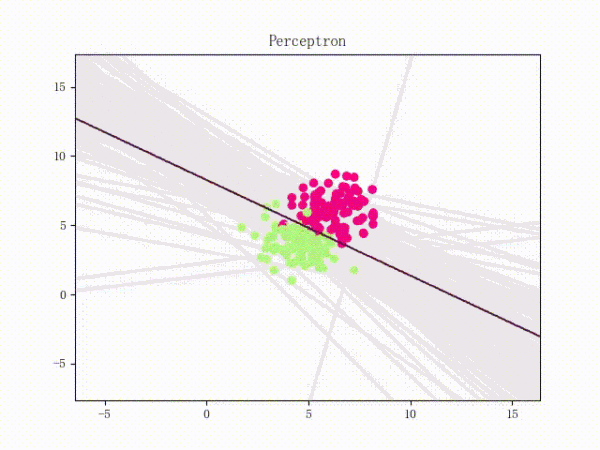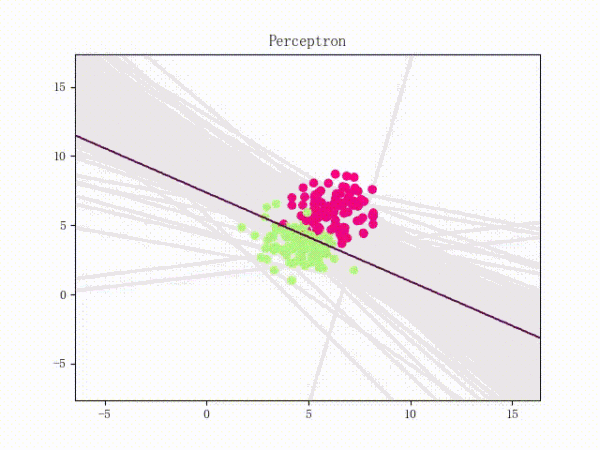
超平面分类的判别方法是通过带入计算正负,比如:
作为1类
作为-1类
感知机的损失函数
感知机的学习过程就是将分错类的数据不断纠正的过程。设分类器对判定的类别是
,而它实际的类别是
,完美情况下当然希望所有点都能满足
。
即使不完美我们也知道一个好的分类器会有这两个特性:被分错的点尽可能少,即使被分错了,也距离超平面非常近。能够描述这两个的特性的,就是被分错的点到超平面的距离之和。所以可以把这个距离之和作为损失函数。
点到超平面的距离为:, 注意它是有正负的,1类的点到超平面的距离为正,-1类的点为负。我们关注被分错的点,不管是1类点被错分到-1类,还是-1类点被错分到1类,他们的距离取绝对值都是:
设所有分错的点的集合是,那么所有分错的点到超平面的距离和是:
忽略常数项 =>
对损失函数求导:
也就是说参数更新公式为:
的更新如果细化到每个维度,就是:
训练过程
输入:m个n维度的线性可分的已经标好label的数据集,
只有1或-1两种label。
输出:
1) 选择初始值 构建初始感知机分类器
2) 选择数据点进行分类,判断是否为分错的点,即如果
则为分错的点。否则循环2)
3) 更新参数,因为每次只取一个点来更新参数,所以参数迭代公式可以简化为:
4)回到2)直到找不到分错的点
以上。