CART定义
在上一篇决策树中,我们已经介绍了决策树的原理和ID3,C4.5算法。这一篇专门讲解CART算法。
CART即Classification and Regression Tree,分类与回归树。特点是:只有二叉树。
分类树
CART用作分类树的时候跟ID3,C4.5决策树算法类似,只是特征分裂的准则不一样: CART首先是二叉树,其次分裂评价标准是用基尼指数
基尼指数
基尼指数可以用来描述一个集合D的类别纯度,集合的样本们只属于一类,那该集合的基尼指数为0,集合的样本属于越多类,则基尼指数越大。基尼指数对集合的算法是:
该式子的解读:集合的样本属于K个类,现在随机抽取一个样本,它属于第k个类的概率为。设集合里一共有n个样本,第k个类的样本有m个,则
在特征A取值为a的条件下的集合D的基尼指数为:
上面式子中,为A取a时的样本集合,
为其它样本的集合:
可以看到特征A取值之后,影响了集合的密度,形成了
和
两部分的密度,所以需要加权。
分类树特征分裂
我们依然考虑此数据集:
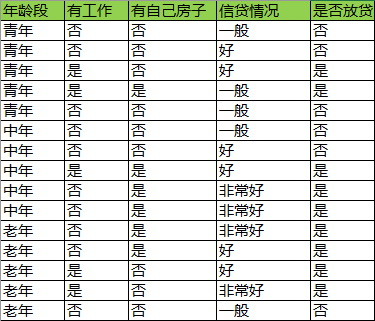
设表示年龄段,有工作与否,有自己房子,信贷情况4个特征。
表示青年,中年,老年;
表示有工作和没工作;
表示有房子和没房子;
表示信贷非常好,好,一般。
1)假设以“青年”与否为分裂点,即,求基尼指数。
2)假设以“中年”与否为分裂点,即,求基尼指数。
3)假设以“老年”与否为分裂点,即,求基尼指数。
4)假设以“有工作”与否为分裂点,即或
,求基尼指数(只有两种情况,基尼指数是相等的)。
5)假设以“有房子与否”与否为分裂点,即或
,求基尼指数。
6)假设以“信贷情况非常好”与否为分裂点,即,求基尼指数。
7)假设以“信贷情况好”与否为分裂点,即,求基尼指数。
8)假设以“信贷情况一般”与否为分裂点,即,求基尼指数。
9)比较以上所有的Gini指数,最小,所以“有房子”与否为最优分裂点
10) 分裂之后的决策图如下:
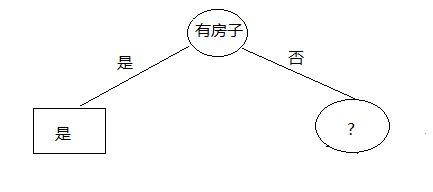
接下来我们继续寻找分裂点进行分裂
目前数据集合被缩小为:
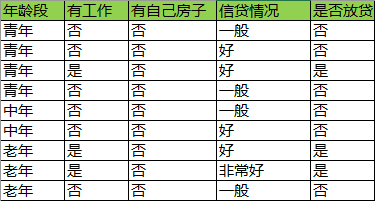
11)以此时的集合为基础,循环到1)开始,计算除了“有房子”与否以外的特征作为分裂点的基尼指数。
中间计算过程省略,直接给出结果:时最小,所以“有工作”与否为最优分裂点。
继续绘制决策图:
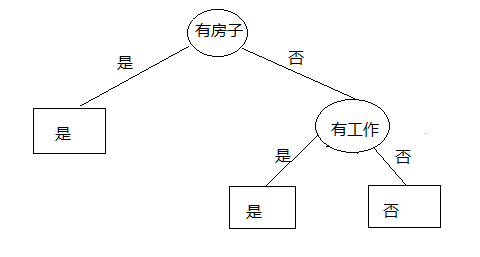
决策完毕。
回归树
回归树结合了线性回归和决策树,本质上是决策树,实现的是分段回归。
对图示的数据点,线性回归为红色,回归树为绿色
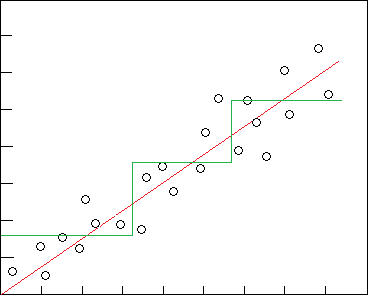
下面开始讲解回归树原理
回归树算法原理
首先对于特征进行二叉特征分裂,先尝试所有分裂点,再通过最小损失函数决定哪个分裂点是最佳的,并进行实质分裂。分裂出来两条分支,每个分支为一个子数据集(这就是为什么上图x坐标是分段的),每个子数据集上的样本的结果都等于它们的平均值(这就是为什么上图y坐标每一段都是同一个值)。然后在每一个子数据集重复上面的的分裂,直到停止条件。 停止条件是人为决定的,比如决定只分裂到第3层。
回归树损失函数
其中的损失函数通过最小二乘法获得,即当同一个点分裂为两个子数据集后,每个子数据集的最小二乘误差最小化,也就是两个子数据集的最小二乘误差的和要最小化。数学表达如下:
上式中为两个子集中计算结果值(即平均值),
为实际结果值
回归树实例分析
考虑以下数据集,x为特征变量,y为结果

绘图为:
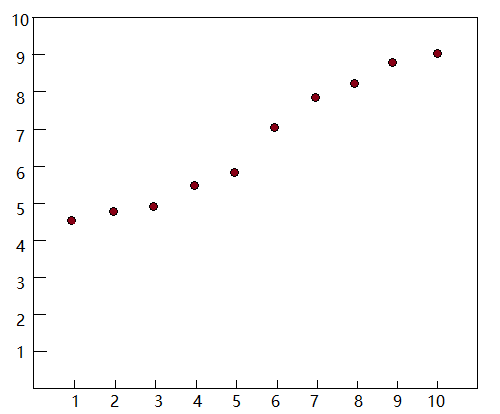
1)只有一个特征变量x,故对它进行分裂。
考虑这9个分裂点 ,之所以不使用1,2,3这种实际特征取值为分裂点,是为了划分子集的清晰。
2) 假设分裂点为,获得两个子集:

计算子集的结果:
计算子集的结果:
计算结果绘制到坐标图中:
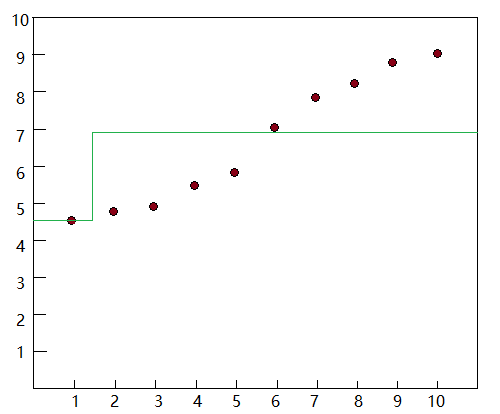
计算这次分裂的损失量:
3) 假设分裂点为,获得两个子集:

计算子集的结果:
计算子集的结果:
计算结果绘制到坐标图中:
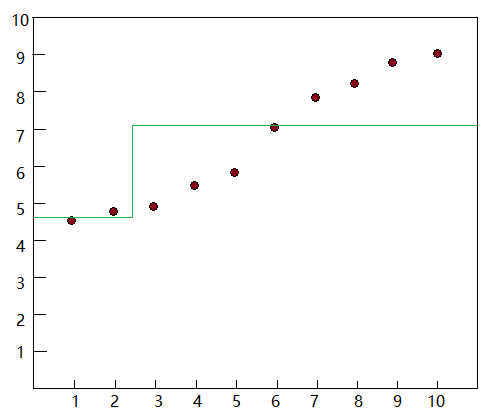
计算这次分裂的损失量:
4)继续计算分裂点时候的结果,得到所有结果为下表:

比较所有损失,当s=5.5的时候分裂,损失最少,所以从s=5.5进行第一次分裂,分裂之后的坐标图为:
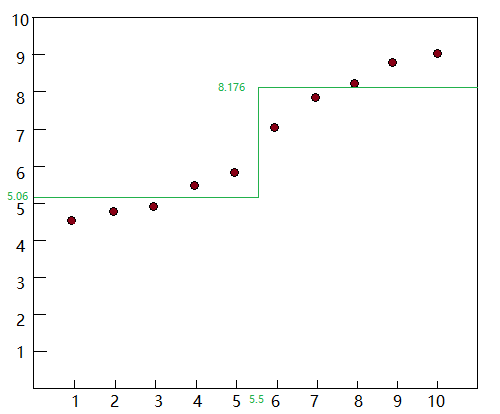
5)至此,数据被分裂为两个子集:

对进行1)~4)的分裂过程,得到:
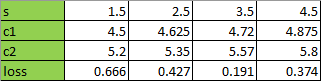
当s=3.5的时候分裂,损失最少,所以从s=3.5对进行分裂
对进行1)~4)的分裂过程,得到:
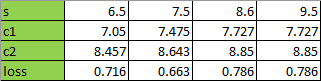
当s=7.5的时候分裂,损失最少,所以从s=7.5对进行分裂
绘制坐标图
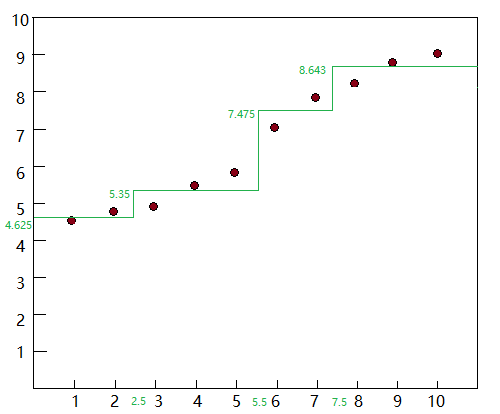
我们看一下此刻的树图:
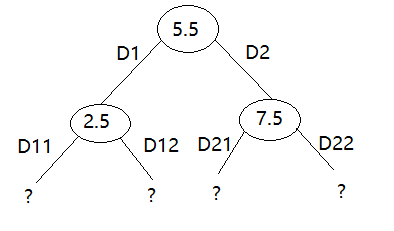
如果觉得目前的回归精度满足要求(比如规定一个子集里面的样本数低于事先设定的阈值),可以就此时终止,则我们的回归树已经构建了3层了(称深度为3。
不过,为了精度再高一点,我们再构建一层。
6)第三层构建开始,目前4个子集为:

对4个子集分别进行1)~ 4)的循环。省略中间过程,直接给结果:

D11: 选择s=1.5分裂
D12: 选择s=4.5分裂
D21: 选择s=6.5分裂
D22: 选择s=8.5分裂
绘制坐标图:
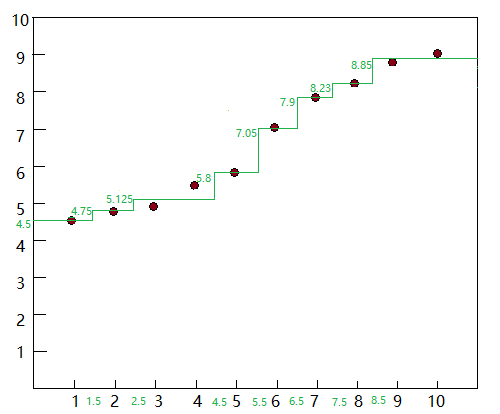
树图:
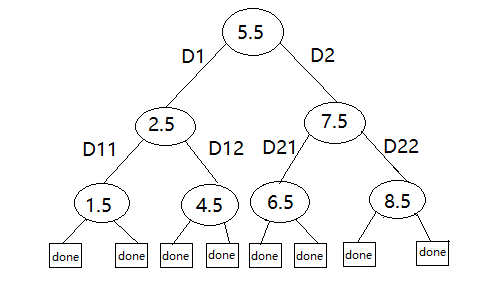
构建完毕。
BTW,事实上D11和D21已经过拟合,因为它本身只有两个边界点,从结果上看loss也已经为0了
剪枝算法
预剪枝
在构建树的过程中依照指定的标准而停止构建某个分支,常用的方法有:
1)定义一个深度,当树到达该深度就停止,如上面用到的
2)定义一个阈值,当某个节点子集的样本数小于该阈值,就停止
3)定义一个阈值,计算每次扩张对系统性能的增益,当增益值小于该阈值,就停止
后剪枝
先构建完整的树(允许过拟合),然后剪掉置信度不够的子树,并用子树种最频繁的类别或值代替
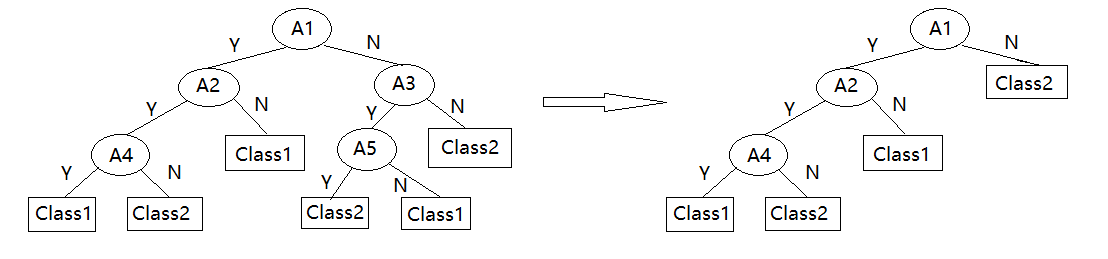
剪枝的方法有:
Reduced-Error Pruning(REP,错误率降低剪枝)
Pesimistic-Error Pruning(PEP,悲观错误剪枝)
Cost-Complexity Pruning(CCP,代价复杂度剪枝)
EBP(Error-Based Pruning)(基于错误的剪枝)