决策树
决策树的定义
决策树类似于人们进行决策的过程,从一个根节点开始,通过逐一特征的筛选,生成多个分支,每个叶子节点为一个分类
考虑下面的样本:
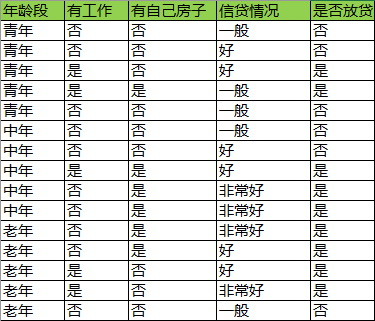
人们的决策过程:
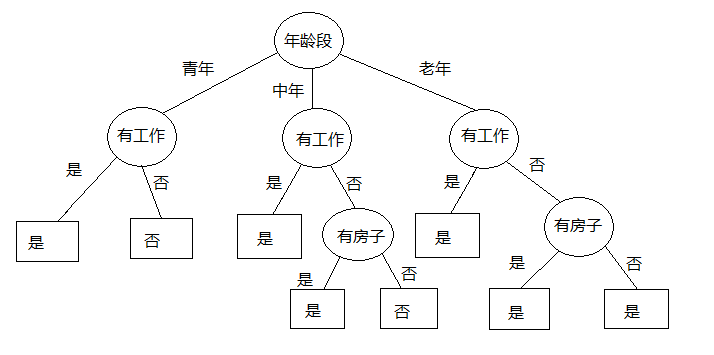
我们看到对于青年来说,只要工作情况就能决定是否房贷,房子和信贷情况并没有起到区分作用。对所有年龄层的来说,信贷情况都是多余的特征。这个决策过程看起来不错,不过这就是最佳路径了吗?
而在实际操作中,我们是用什么算法策略决定每一步特征的选取呢?也就是说,我们进行特征选择是基于什么准则?
特征选择
我们基于信息增益来选择特征。信息增益指的是信息熵的增益,为理解它需要提前了解两个概念:信息熵,条件熵
信息熵
一个事件发生的概率越低,它的不确定性就越强,信息量就越大,所以我们要用概率的函数来表示信息量,即;多个独立事件发生的概率是它们各自概率的乘积,而信息量是他们各自信息量的和,即
满足这个条件的函数是对数,于是用对数表示信息量:
其中
上面说的是一个具体的事件或特征。对一个变量X来说,它可能取不同的值,它取任何一个值都是一个事件,且所有取值的事件互相独立。我们考虑X的信息就应该考虑它所有取值,那么合理的方式就是使用它所有取值信息量的期望:
我们将此称作信息熵。所以说信息熵指的是变量的属性。
条件熵
现在在X基础上再加入另一个变量Y,它们的联合概率分布(与条件概率分别的区别见附录)为
定义条件熵为Y在X条件下的熵:
其中
观察条件熵的定义公式,从外往里看,它是X取值变动下对熵的加权和,而本身
是固定
下的,Y取值变动下每个条件概率
的加权和。所以它是期望的期望,或者说是熵的熵,是信息量的嵌套加权。
推导一下条件熵具体的计算方法:
则:
①
②
由②可见条件熵由联合概率和条件概率构成。由①可见,条件概率可以由联合概率和作为条件的事件概率求得
信息增益
了解了信息熵(或者称经验熵)和条件熵,可以来理解信息增益了。
信息增益的定义是,当一个特征A引入后,原来集合D的经验熵,变成了D对A的条件熵,这个变化过程熵减少了多少。用数学表示:
BTW,因为特征在不断引入,每次引入之后的条件熵就成为下一次特征引入前的经验熵。
决策树的特征选择基于信息增益最大,也就是新特征的加入使得整个集合的信息量减少最多,概率就越大,这样就越接近最终分类结果。
基于信息增益进行特征选择
现在开始通过计算信息增益来对上述样本进行特征选择。
1.1)首先计算初始经验熵,初始只有一个特征D,就是放贷与否。放贷为,不放为
,则经验熵为:
1.2)假设引入“年龄段”特征。则原来对样本的了解只有放贷与否,现在多了一个“年龄段”的区分度。设“年龄段”为,使用上述②式,计算条件熵:
P(青年,放贷)= P(放贷|青年)=
P(青年,不放贷)=
P(不放贷|青年)=
P(中年,放贷)= P(放贷|中年)=
P(中年,不放贷)=
P(不放贷|中年)=
P(老年,放贷)= P(放贷|老年)=
P(老年,不放贷)=
P(不放贷|老年)=
=>
1.3)假设引入“有工作与否”特征。设“有工作与否”为,使用上述②式,计算条件熵:
P(有工作,放贷)= P(放贷|有工作)=
P(有工作,不放贷)=
P(不放贷|有工作)=
P(没工作,放贷)= P(放贷|没工作)=
P(没工作,不放贷)=
P(不放贷|没工作)=
=>
1.4)假设引入“有房子与否”特征。设“有房子与否”为,使用上述②式,计算条件熵:
P(有房子,放贷)= P(放贷|有房子)=
P(有房子,不放贷)=
P(不放贷|有房子)=
P(没房子,放贷)= P(放贷|没房子)=
P(没房子,不放贷)=
P(不放贷|没房子)=
=>
1.5)假设引入“信贷情况”特征。设“信贷情况”为,使用上述②式,计算条件熵:
P(信贷一般,放贷)= P(放贷|信贷一般)=
P(信贷一般,不放贷)=
P(不放贷|信贷一般)=
P(信贷好,放贷)= P(放贷|信贷好)=
P(信贷好,不放贷)=
P(不放贷|信贷好)=
P(信贷非常好,放贷)= P(放贷|信贷非常好)=
P(信贷非常好,不放贷)=
P(不放贷|信贷非常好)=
=>
1.6)比较,
,
,
=>
也就是这里我们选择特征“有房子与否”,至此我们做出了第一个特征选择,在选择之后根据有房子与否的“是”与“否”岔开了两个路径,也就是分割出来了两个子空间和
,其中“是”空间的路径已经抵达了叶子;“否”空间还有待开发。
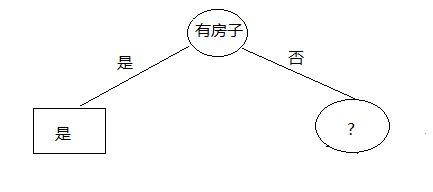
2.1)针对分出来的子空间,继续进行特征选择。
幸运的是,我们只有一个子空间需要开发。
空间的数据缩小为:
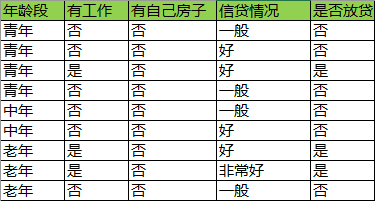
此时空间处于初始状态,即没有选择任何特征,它的信息熵为:
2.2)假设引入“年龄段”特征。设“年龄段”为,使用上述②式,在
数据空间计算条件熵:
P(青年,放贷)= P(放贷|青年)=
P(青年,不放贷)=
P(不放贷|青年)=
P(中年,放贷)= P(放贷|中年)=
P(中年,不放贷)=
P(不放贷|中年)=
P(老年,放贷)= P(放贷|老年)=
P(老年,不放贷)=
P(不放贷|老年)=
=>
2.3)假设引入“有工作与否”特征。设“有工作与否”为,使用上述②式,计算条件熵:
P(有工作,放贷)= P(放贷|有工作)=
P(有工作,不放贷)=
P(不放贷|有工作)=
P(没工作,放贷)= P(放贷|没工作)=
P(没工作,不放贷)=
P(不放贷|没工作)=
=>
2.4)假设引入“信贷情况”特征。设“信贷情况”为,使用上述②式,计算条件熵:
P(信贷一般,放贷)= P(放贷|信贷一般)=
P(信贷一般,不放贷)=
P(不放贷|信贷一般)=
P(信贷好,放贷)= P(放贷|信贷好)=
P(信贷好,不放贷)=
P(不放贷|信贷好)=
P(信贷非常好,放贷)= P(放贷|信贷非常好)=
P(信贷非常好,不放贷)=
P(不放贷|信贷非常好)=
=>
2.5)比较,
,
=>
所以我们选择的特征是“有工作与否”,并且注意,该特征的信息增益是,意味着,全部信息被衰减,流程图应该停止了。我们绘图看看是否如此:
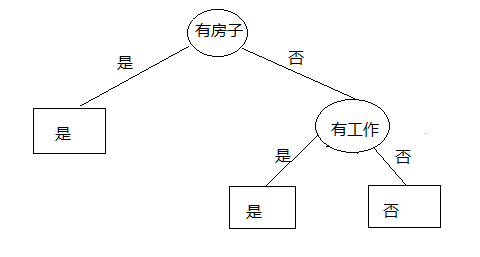
的确如此!
我们比较此图和初始的流程图,可知,采用信息增益,可以尽可能等减少分支和叶子,迅速决策。
决策树生成算法
常见的决策树生成算法有ID3算法,C4.5算法和CART算法
ID3算法
ID3算法使用的是信息增益,其运算过程正是上节所描述的例子!
C4.5算法
C4.5与ID3的区别仅仅是使用信息增益比 而非信息增益。为什么要用信息增益比呢?
因为在使用信息增益,会导致特征选择时偏向于选择取值较多的那个特征,而那个特征可能是没有意义的。比如编号,身份证号,星期几。如下的用星期作为特征,可以产生5个分支,使用ID3算法的信息增益可以将所有信息熵衰减掉,直接生成五个叶子:
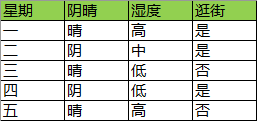

这是非常严重的过拟合。为了避免这种情况的产生,我们必须增加与分支数(选定特征的取值数)相关的惩罚项,形成信息增益比:
其中惩罚项是,
是所选特征的取值数,
是子空间,此例中
CART算法
将会在之后的文章中单独讲解
说明
当然,需要注意的是:无论使用哪种算法,对于大数据来说,我们的决策树的层数可能非常多,如果我们分解到没有特征可分的地步会过拟合,且时间消耗非常大。 通常的做法是设置一个信息增益阈值,当某个特征引入后信息增益小于该阈值
,我们就可以停止树分裂,并把原始数据集中数量最多的那个类别作为叶子节点
附录:联合概率分布和条件概率分布的区别
考虑两个变量:天晴与否,花开与否
它们组合成四种事件:
1)天晴了A1,花开了B1
2)天晴了A1,花没开B2
3)天没晴A2,花开了B1
4)天没晴A2,花没开B2
联合概率分别描述这四种情况:
,
,
,
,
条件概率分布描述的是某个事件已经发生了,比如B1已经发生了,就扼杀了2),4)的可能,我们就只能从1),3)两种情况去考虑:
,
条件概率和联合概率的数学关系:
参考
《统计方法学》by 李航