PCA主成分分析

降维思想

PCA即Principal Component Analysis, 主成分分析。主要思想是数据降维。

降维的办法常常是利用现有的n维数据的统计特征，创造更少的m维特征来表示该组数据，实现降维。

有三个数据点在正交基下表示为

我们可以用2x3矩阵来表示它：

这里我们发现数据的x与y两个维度有着规律：x=2y，则我们可以创造出新的维度 :

在新维度下表示数据只需要1x3矩阵：

至此，实现了降维。

最大方差

上面是一种特殊情况，即所有数据点恰好在一个向量方向上。通常情况，我们有很多数据点且并非所有数据都能连成一条线。

这时候我们要找到一个维度（一个向量），让所有数据投影（降维）到该向量上之后，尽可能地分散。因为越分散说明通过该向量降维之后数据得以很好地区分，越紧凑说明该降维导致了越多信息丢失。数学上表达“分散”的方式就是：方差。方差越大，则说明数据越分散

为了计算方差方便，对数据进行去均值（即以各维度的均值所指明的点为中点）。接下来我们要找到一个单位向量（为了计算方便）使得投影后数据最分散，即方差最大：

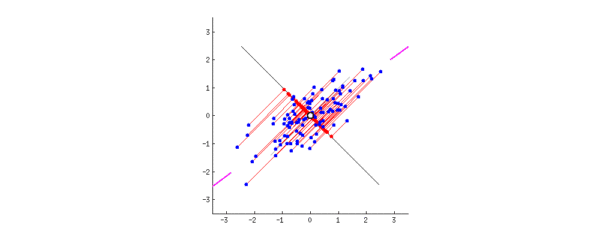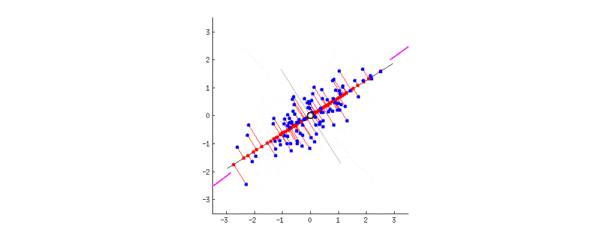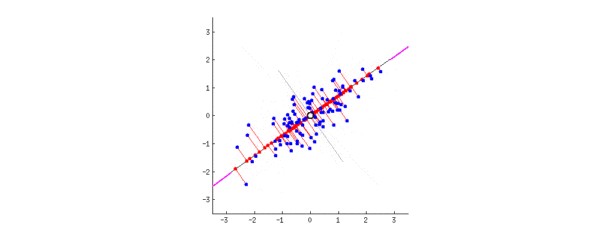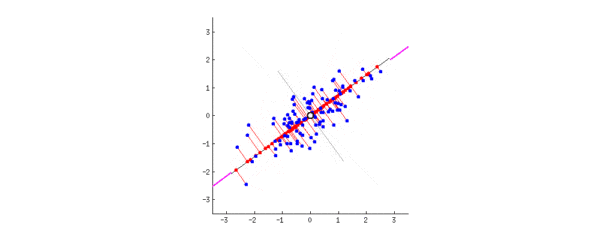
设该向量为, 数据点为向量（以中心点为原点作向量）

通过向量点积求投影长度：

则方差为:

                       

                       

                       

设， 则C为协方差矩阵。为什么呢？推导如下——

对于一个有m个n维样本的样本集，我们把它写成行向量形式（只是为了方便观察，写成列向量也可以。并不影响协方差矩阵的shape），即每行为一个样本，每一列为一个维度，且维度分别为D1,D2,…,Dn：

求该样本集的协方差矩阵：

        

        

常数项不重要，将其隐去，则 推导完毕。

回到上面的方差公式：

所以接下来我们要求取一个单位向量（即约束条件：）使得方差最大

采用拉格朗日乘子法,即转换为求如下函数的极值：

求极值，则要求偏导数为0：

顺便提一下的求导过程，利用了协方差矩阵C为对称实矩阵的特性，不然你得不到这么完美的结果的。

同时，恰好是特征向量和特征值的定义！

于是，上面的极值条件转换为：

求协方差矩阵C的单位特征向量

不过，特征向量和特征值那么多，哪一个才是使得方差最大呢？

所以，最大特征值对应的特征向量使得方差最大，也就是使得数据降维之后最分散。

不过在实际PCA应用中，一般不会直接降维到只有一个特征向量。降维是为了在容许丢失部分信息的前提下简化数据复杂度，不是为了简化数据复杂度而去一味地降维。于是，我们会从大到小，选则m个最大的特征值对应的特征向量，组成新的m组维度，来表示原始数据。在PCA里称这是m个主元。

协方差矩阵的意义

以二维为例，在数据图形中理解协方差矩阵：

协方差矩阵对角线上为x方向和方差，它表示x轴方向和y轴方向数据的散度。非对角线上为x,y方向相关度：0表示无关，数据在x轴上延伸，在y轴上无变化；正数表示正相关，数据在x轴正向延伸，在y轴也正向延伸，且越大表示相关性越大；负数表示负相关，数据在x轴正向延伸，就在y轴负向延伸。

在特征向量方向重新表述上面的散度关系，同时利用上面的结论，我们得到以下结论：特征向量方向的数据方差大小为对应的特征值；两个特征向量方向数据的协方差为0

我们继续在数学上解释以上结论——

首先找到协方差矩阵的特征向量和特征值，也就是把原矩阵对角化为： （为特征向量组成的正交矩阵，为对应的特征值组成的对角矩阵）。接下来我们从相似矩阵的意义去理解，即：从特征向量组成的新基的视角看矩阵C，是的样子。所以是特征向量视角下的新的协方差矩阵。 它的对角线元素表示在特征向量方向的数据散度（方差），非对角线元素表示两个特征向量方向上数据相关性，在这里它为0，说明不相关。

这个结论也正好反过来说明了，我们用找到的特征向量作为新的主元，足以表示数据的特征。接下来要做的当然就是选取最大的m个维度进行降维了。