引入
在之前的SVD Decomposition一文中,我们介绍过,一个mxn的矩阵A可以分解为:
其中为
的特征矩阵,
为
的特征矩阵。同时我们通过选取部分奇异值及其对应的特征向量的方式实现对
的降维:
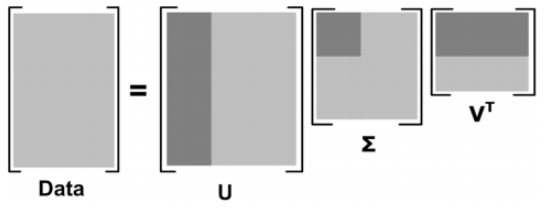
这一降维方式可以运用在图像压缩中。
此文中,我们将继续探索SVD降维方法在推荐系统中的应用。
推荐系统实践
问题的提出
我们考虑这样一个评分样本,6个user对5个item分别进行了评分,没有评分的计作0分:

接下来,我们的目标是向user_5推荐item。应该向Ta推荐item_1,还是item_5呢? ——
这里采用的策略是:找到与user_5喜好最接近的用户,然后把该用户对item_1, item_5中评分最高的那一个推荐给user_5。于是问题转化为:哪个用户与user_5的喜好最接近?
在实际应用中,user-item数据表的维度远远大于6x5。在巨大维度下,计算成本太高,使用SVD进行降维后再计算,是推荐系统里常用的方法。
SVD求解
首先将样本数据看做一个矩阵6x5的矩阵并进行SVD分解:
对于评分矩阵,该分解意味着什么呢?我们来计算一下user_3对item_2的评分

=>
也就是说A中各个位置的元素来自于的对应位置行向量和
的对应位置列向量按照奇异值进行加权点积。
将的行向量看作user向量在新特征下的表示,
的列向量看作item向量在新特征下的表示,同时只截取权重最大的前两个特征,对数据进行降维:

=>

至此,实现了降维。
我们在此维度下,寻找与user_5最接近的user。每个用户向量抽离出来是2维向量:
然后我们要找出与向量相似度最高的向量。
向量的相似度是怎么评估的?—— 评估标准有很多种,常见的有:夹角余弦法,欧氏距离法等。这里我们使用欧式距离,即两个向量和
之间的欧式距离为:
欧式距离越小,向量相似度越高。
通过计算得知,与
相似度最高,所以user_2和user_5的喜好最接近。
回到原始矩阵看user_2对item_1和item_5的评分:item_1评分,更高。 因此将item_1推荐给user_5。
向新用户推荐item
上面求解的是向已知用户推荐item。如果现在有一个新的用户,它的数据并不在上面的样本矩阵里,怎么办?
容易想到的是,直接加入原样本数据进行扩展再求解,但是这样做在大数据情况下时间消耗太大。我们需要基于已经有的模型对新加入的用户进行item推荐。
首先,将新用户投影到降维后的user向量空间中去(为什么是这个算法?我也在找寻答案 请见附录):
接下来通过欧式距离或者其它方式,找出 ~
中与
相似度最该的且对item_2和item_5评过分的user, 然后把该user对item_2和item_5中评分更高的item推荐给
用户
以上。
附录
将SVD分解的原始矩阵A和分解矩阵U都写成行向量形式:
=>
=>
=>
=>
上述即原始user向量向新特征下的user向量的转换公式。
将SVD分解的原始矩阵A和分解矩阵都写成列向量形式:
=>
=>
=>
=>
=>
上述即原始item向量向新特征下的item向量的转换公式。