Matrix Multiple by CUDA Shared Memory 使用共享内存优化矩阵相乘

Posted on | In | Views:
CUDA

本来来自对于CUDA中使用shared memory进行矩阵相乘的思考。之所以写下它，是因为我感觉到这个例子代表着cuda处理矩阵的基本思维方式，掌握它，时常复习它，很有必要。

目标是实现矩阵相乘：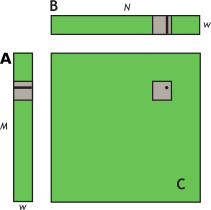

它是如何思维的：
1）全局看，gridDim是完全映射输出的矩阵C，基于定义了C的row, col两个变量
2）局部看，每个block大小为TILE_DIM*TILE_DIM, 也就是w*w, 对应矩阵C的一个TILE_DIM*TILE_DIM区域，而该区域来源于A和B对应的区域。所以把眼光缩小到这几个区域来，在一个block中设计算法即可。
3）以上两点即完成了对矩阵乘法的cuda化拆分。而shared memory的加入只不过是为了提高读写效率而已

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
__global__ void sharedABMultiply(float *a, float* b, float *c, int N)
{
    // Actually TILE_DIM==w
    __shared__ float aTile[TILE_DIM][TILE_DIM],
                     bTile[TILE_DIM][TILE_DIM];
                     
    // grid view: gridDim is exactly mapped to Matrix C
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    float sum = 0.0f;
    
    // block view: each block is a TILE_DIM*TILE_DIM erea of Matrix C
    aTile[threadIdx.y][threadIdx.x] = a[row*TILE_DIM+threadIdx.x];
    bTile[threadIdx.y][threadIdx.x] = b[threadIdx.y*N+col];
    __syncthreads();
    for (int i = 0; i < TILE_DIM; i++) {
        sum += aTile[threadIdx.y][i]* bTile[i][threadIdx.x];
    }
    c[row*N+col] = sum;
}

代码上的难点，在于传入kernel的矩阵a,b内存是扁平化为一维的，读写需要进行索引转换。
我们可以先假设它是二维：

1
2
aTile[threadIdx.y][threadIdx.x] = a[row][threadIdx.x];
bTile[threadIdx.y][threadIdx.x] = b[threadIdx.y][col];

然后再转换为一维：

1
2
aTile[threadIdx.y][threadIdx.x] = a[row*TILE_DIM+threadIdx.x];
bTile[threadIdx.y][threadIdx.x] = b[threadIdx.y*N+col];

以上。