卷积和神经网络
卷积
了解卷积神经网络(Convolutional Neural Network)之前先来了解卷积。见下图:

从上图看,一个矩阵被另一个矩阵(我们称作“卷积核”)执行卷积,就是中矩阵通过一定步长(图中步长为1,也就是每次移动一个元素)扫描左矩阵,每次停留时计算对应元素的乘积之和作为新矩阵(右)的元素。
具体的计算例子:
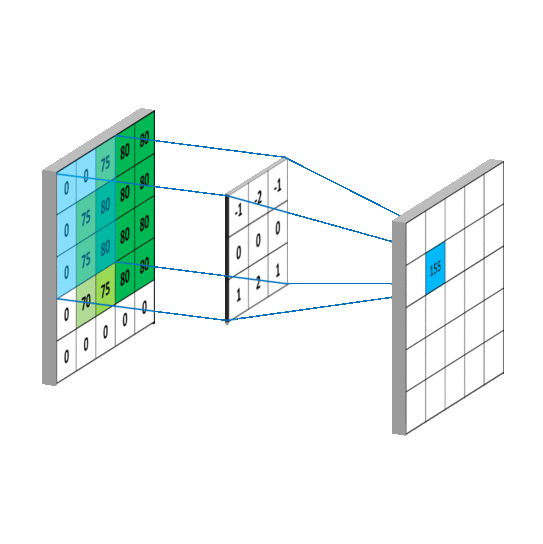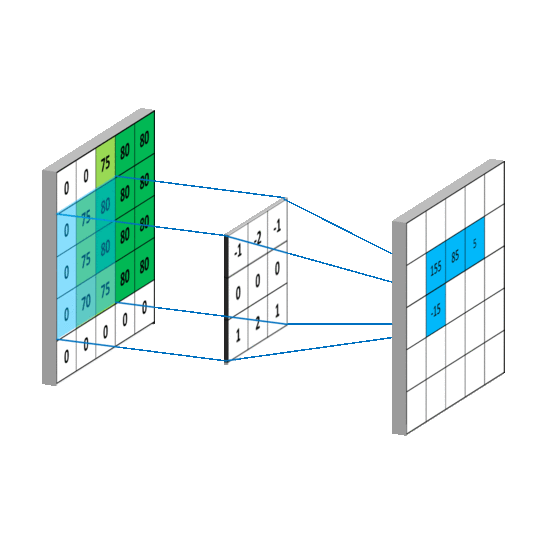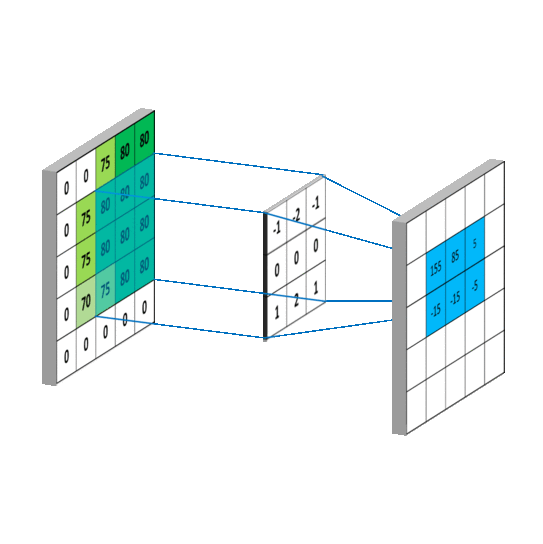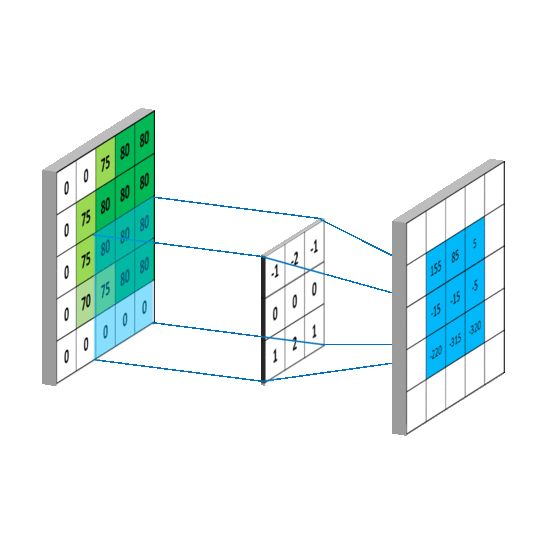
卷积的神经网络表示
那么卷积计算如何使用神经网络来构建呢?在之前的blog里讲过神经网络是加权求和,于是我们可以这么构建:
实现的神经网络为:
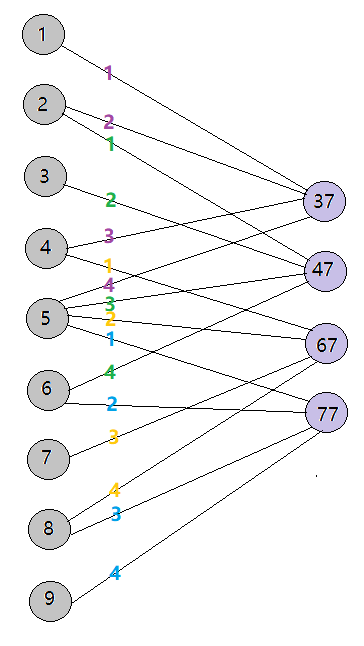
CNN的各层
CNN是因为有卷积层才叫CNN,但是除此外通常还有几个层:线性整流层,池化层,全连接层。至于它们的组合顺序和个数,取决于不同网络设计方式。只要它有效,任何组合方式的CNN网络都可以被认可。
我们假设输入为图像,来讲讲常见的构造:卷积层->线性整流层->池化层->全连接层
卷积层
正如上面的例子讲过的,卷积层是对各个像素进行加权求和,而权重就是卷积核(或称作感受野)的元素。卷积层的物理意义就是提取图像各个部分的特征
线性整流层
整流层采用激活函数进行激活,常用的是Relu函数,它的图像如下:
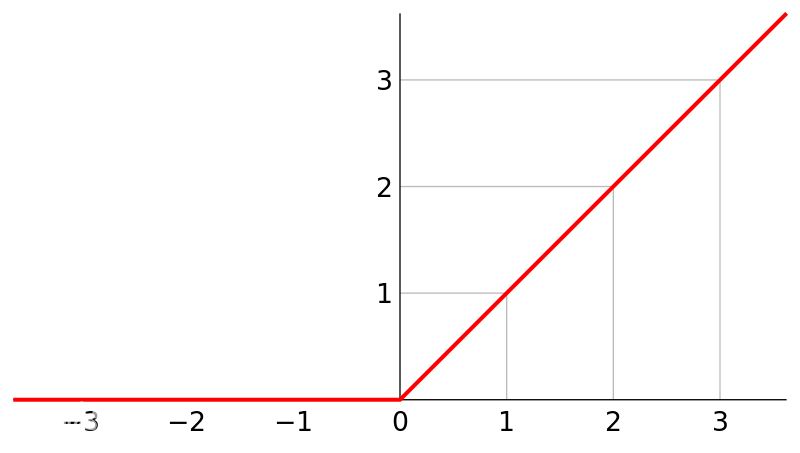
为什么选择Relu? 因为:
1)信号通过它之后等于设置了阈值,在小于阈值(比如小于0),信号完全衰减。换句话说,不是所有信号都去拟合,这样有助于防止过拟合
2)它的导数大部分为常数,反向传播时计算量大大减小
3)它不像Sigmoid等激活函数,越往后导数越接近于零,容易造成梯度消失。而梯度消失会导致参数没法更新,训练停滞
很多情况下,习惯将线性整流层并入卷积层的。所以在有些文档里,我们不会看到“线性整流层”
池化层
池化层是为了保留主要的特征,缩减数据量,减少下一层的参数和计算量,防止过拟合。常用的有mean-pooling和max-pooling
2x2平均池化:
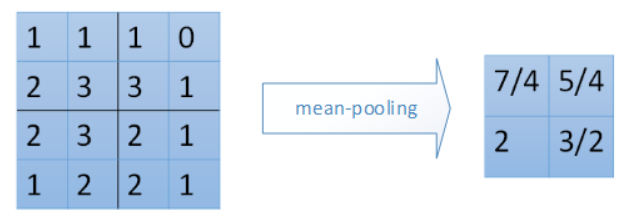
2x2最大池化:

全连接层
卷积层和池化层都是对局部的操作,而全连接层得以将全局进行加权求和。全连接层常常是放在神经网络的最后一层或接近最后(后面不会再接卷积层了),因为我们轻易不进行全连接,只有最后需要输出预测了才进行全局整合。
另外,这里有一个trick: 我们可以把全连接层理解为特殊的卷积层,即感受野和原矩阵一样大的卷积层!
网络优化
出了常用layer之外,我们在进行CNN构造或者训练的时候常常会使用一些有效的方法:
Padding
通常说的Padding是zero-Padding,也就是补零。它是对被卷积图像边缘进行补零扩充的方式。
为什么要补零呢?
因为不补零的话,卷积的结果矩阵的size会比原矩阵缩小(且在stride步长越大的情况下,缩小越厉害),造成信息的损失
为了保持矩阵一致,我们使用zero-Padding。示例如下:
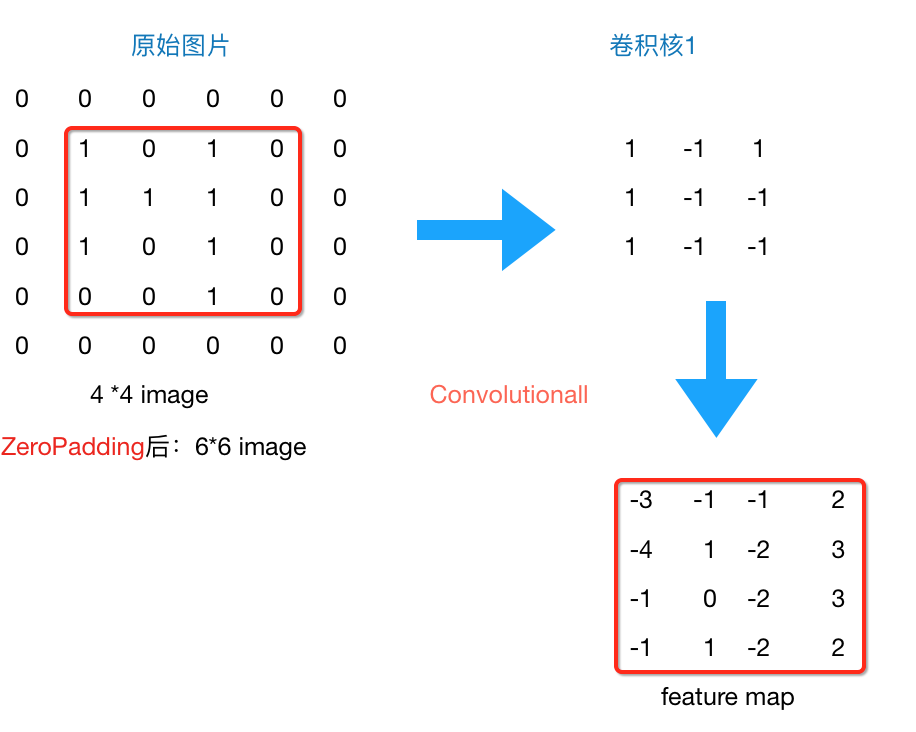
参数共享
参数共享指的是,每一层的卷积操作,我们只使用一个卷积核对所有的输入进行操作。我们并不会在移动一个步长之后变换卷积核中的元素值,这样对于该层的权重来说,它是权值共享的。
为什么要参数共享呢?一方面是为了能够减少计算量,另一方面从意义上说,我们可以看做一个卷积核的操作是“一类”特征的提取。我们“公平地”使用同一个卷积核对整张图片的所有部分进行特征提取。
参数共享不代表特征提取就单调了,因为可以再定义一层多层卷积,使用不同的卷积核进行不同的特征提取。
训练优化
除了网络结构上的优化,在实际训练中也有很多有效的tricks。
这里的训练优化已经不是针对于CNN了,在神经网络中有普遍的应用
Dropout
深度神经网络的普遍问题就是训练时间长和过拟合,为了减少这些问题,Dropout是有效的方法之一。
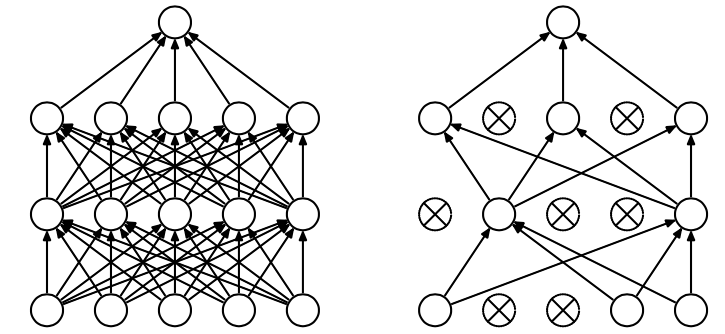
Dropout是指在训练中基于dropout rate随机丢弃元素,使得网络简化,而且因为每轮训练丢弃的元素不同,所以每轮保留的特征是不同的,这样训练出来的模型范化性更强。示例如下:
Early Stop
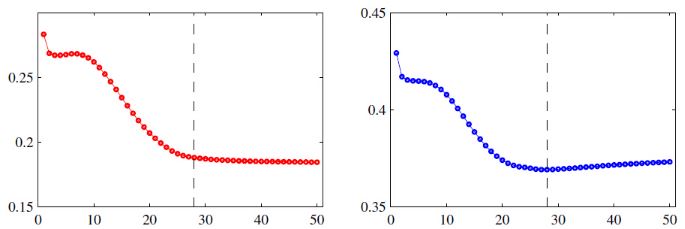
训练中,我们常常会将数据集分割训练集和验证集。Early Stop的提前终止思想是在验证集上的错误率到最小时停止训练(是的,一般来说验证集的错误率会先达到最小),而不要等到训练集的错误率到最小时(这时候验证集错误率已经变大了)再停止训练,不然过拟合几率更大
如图,左为训练集错误率,右为验证集错误率。虚线为Early Stop的点:
Data Augmentation
数据增强很好理解:有更多数据当然就能训练出更好的泛化模型。
但问题是,我们如何获取“有用”的数据。常用的方法是:
1)图像的扭曲,旋转等变换,加光照,改变颜色。
2)添加噪声
3)利用GAN生成
Weight Decay
权重衰减指的是在每次使用梯度下降进行权值更新过程中,对权值更新值的过大进行限制
也就是对中的
乘以一个介于0到1之间的值,用来衰减权值,于是得到:
这样的话防止权值过大。
权值过大,就是意味着当前训练出来的模型非常依赖某个或某些位置的元素,也就意味着训练过程中出现了明显的倾向。这是overfitting的表现。
上面是对于每次局部进行衰减,下面讲全局的正则化方法:
L2正则化
对全局的损失函数加一个对权值过大的L2惩罚项,也就是各个权值的平方和:
当从这样一个损失函数推导出来的导数被用于梯度下降的参数更新,会是什么样的效果呢?
首先,求任意一个权值求偏导:
其中为惩罚因子,
为权值个数。
获得它的更新公式:
其中小于1,实现了参数衰减,跟上面的参数衰减是一样的!
再来看偏置的偏导:
所以此正则对偏置没影响。
L1正则化
与L2类似,只是惩罚项关于权值是一次的:
首先,求任意一个权值求偏导:
其中表示取
的符号,输出为1或-1
获得它的更新公式:
当为正时,更新后的
变小。当
为负时,更新后的
变大。因此它的效果就是让w往0靠,实现了权值衰减。
Learning Rate decay
梯度下降训练在进行到后期,越来越接近最优值,权值更新的震荡越大,这个时候需要把学习率给衰减,以求更快更准确地抵达最优值:
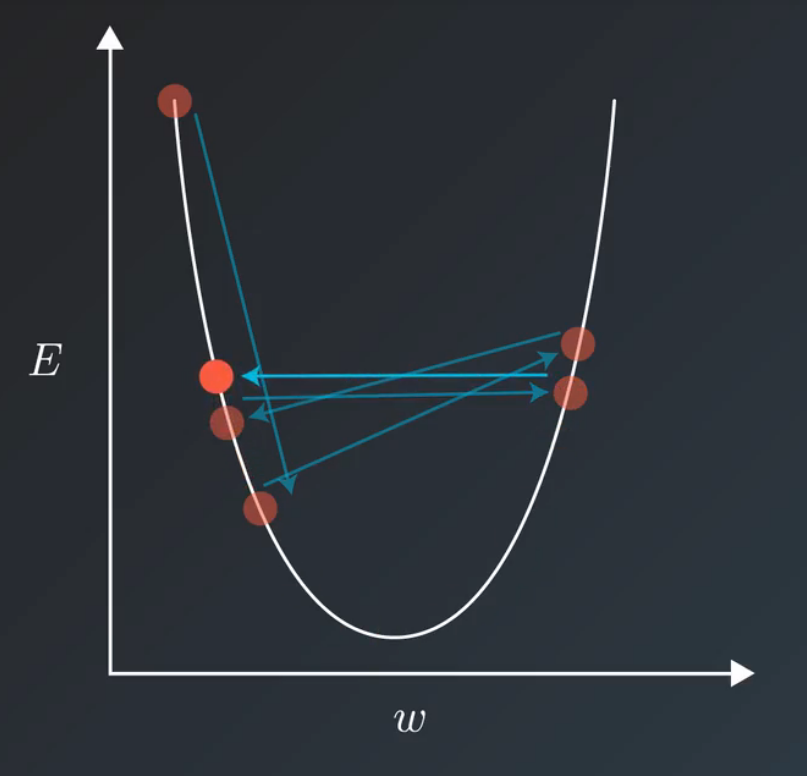
学习率的衰减一般采用的方式:
1) 线性衰减, 如:每5个epochs学习率减半
2) 指数衰减,如:每5个epochs将学习率乘以0.9,也就是衰减率为0.9
注:一个epochs就是把样本数据过了完整一般的意思
各种CNN
CNN是关于卷积神经网络的统一概念,它的构造方式常常如下:
INPUT -> [[CONV -> RELU]*N -> POOLING]*M -> [FC -> RELU]*K -> FC
其中INPUT是输入,CONV表示卷积,POOLING表示池化,FC是全连接,N,M,K是循环数
到底哪种构造最好呢?答案是不知道。网络的构造没有公式,哪个有效哪个更好。于是在前人的实践中,产生了众多有效的优秀的CNN网络:
LeNet (1986)
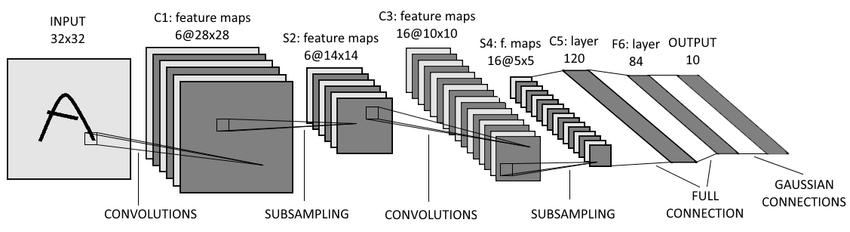
论文在此
AlexNet (2012)
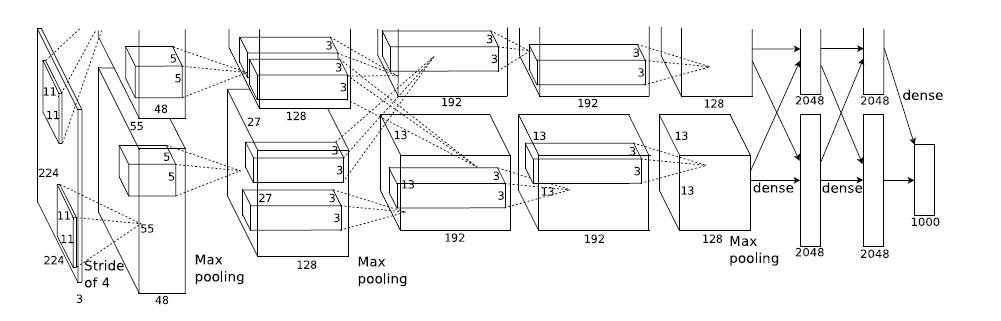
论文在此
VGGNet (2014)
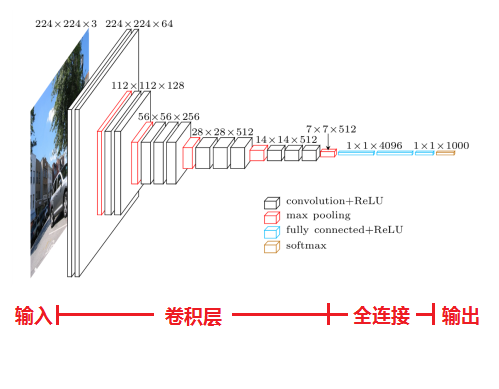
论文在此
GoogleNet (2014)
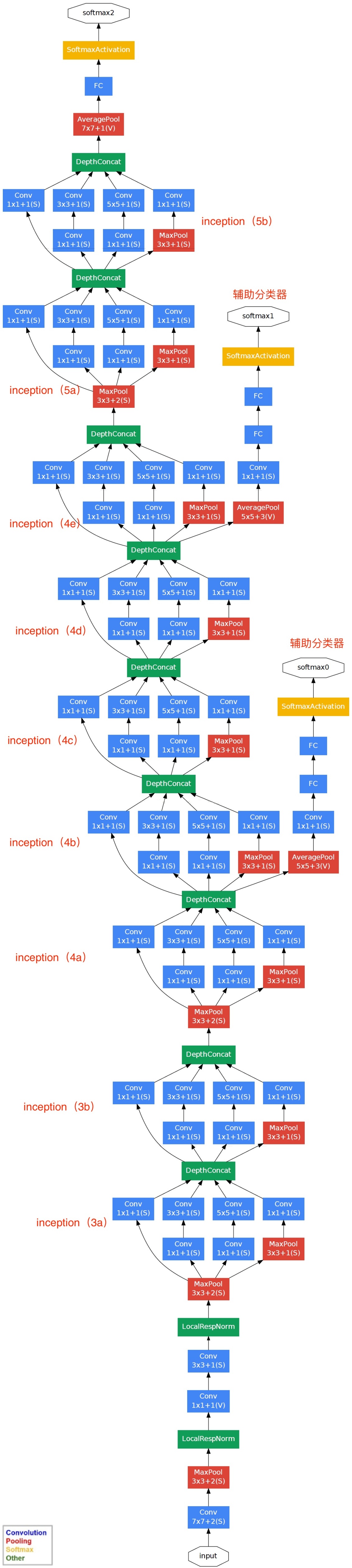
论文在此
ResNet (2015)
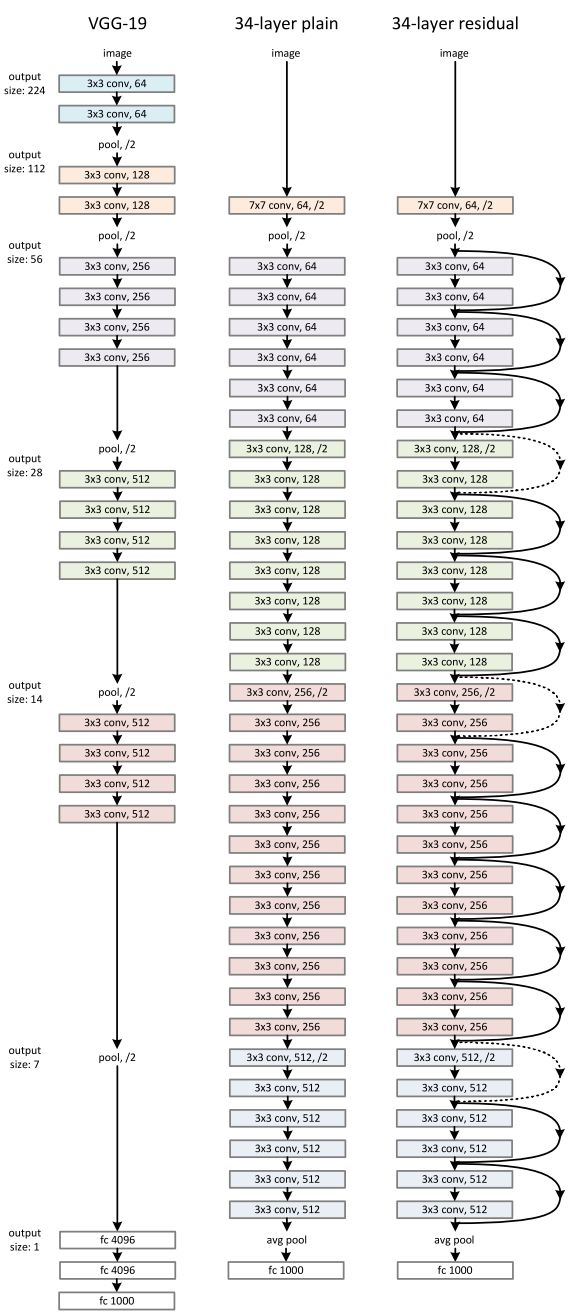
论文在此
以上。