神经网络结构
神经网络的结构如下
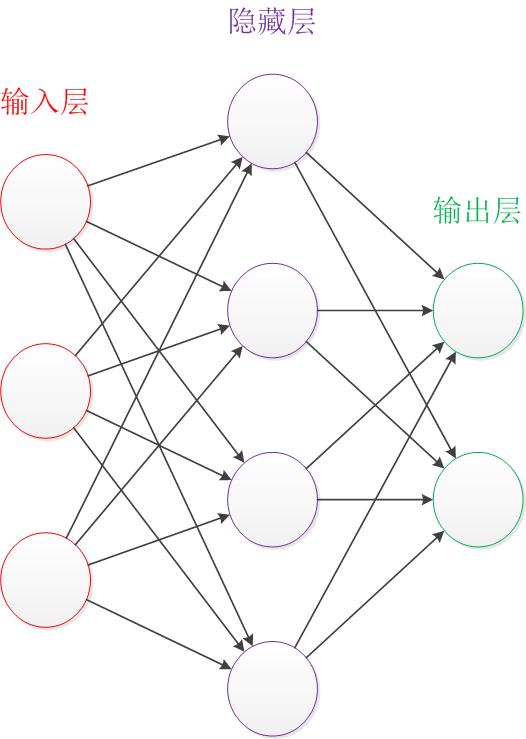
我们只需要从这个图中得到这几点:
1) 输入和输出的个数是固定的
2) 隐藏层是可变的,它的变化就是神经网络设计结构的变化
3) 连线是权重
4) 连线的交汇圈包含求和以及激活函数,是输出,也可以作为下一个隐藏层的输入
5) 圆圈的发散出的多条连线是同一个输入的多份拷贝
关于权重和激活函数,见展开说明的神经网络图:
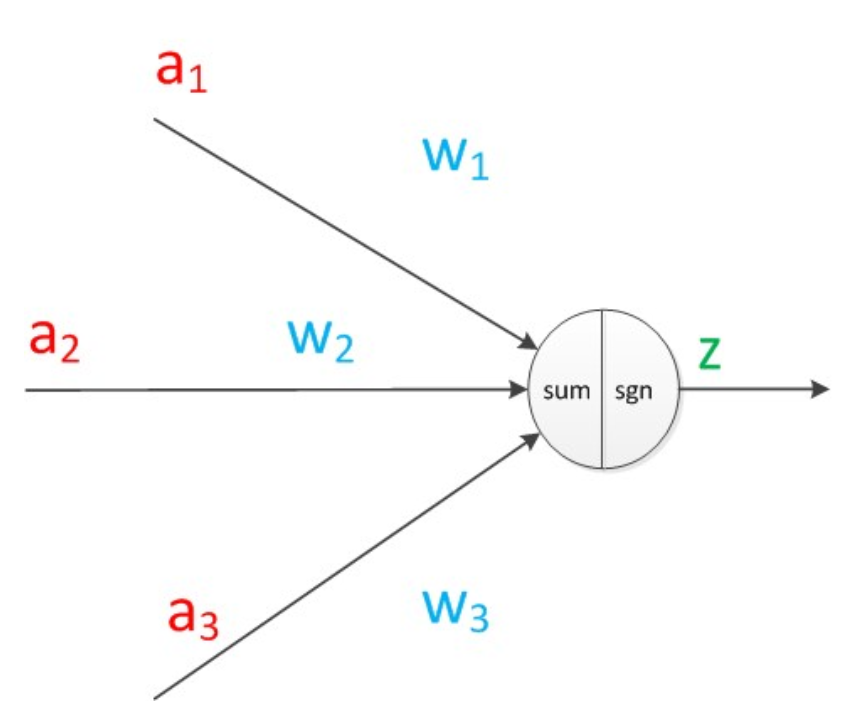
于是上图的代数关系是:
那么sgn是什么呢?根据需要,它可以原样输出,也可以是具体的激活函数函数,比如你定义的输出是概率,那么可以使用sigmoid函数,用来把量值映射到0到1之间。
插一句,在我看来,激活函数是神经网络的精髓,因为它模拟了神经元的工作方式:输入汇集了,不代表神经元会继续传播它,需要看有没有达到阈值,就算达到阈值了,传播出去的信号不一定是原本的量值,而是通过一定规则转换的。
看到求和,很容易想到之前讲过的感知机,而看到sigmoid又想到逻辑回归。它们跟神经网络有什么关系呢?来探个究竟:
感知机和神经网络
一句话:感知机就是神经网络!
在感知机的分类中,是找到一个超平面,( 其中
)来准确地将所有两类数据准确区分在超平面的两边。
也就是说一个点被感知机分类,也就是判断:
是一类
是另一类
用神经网络表示如下:
我们构建一个神经网络:n个输入是,权重分别是
,求和之后,sgn为原样输出,则:
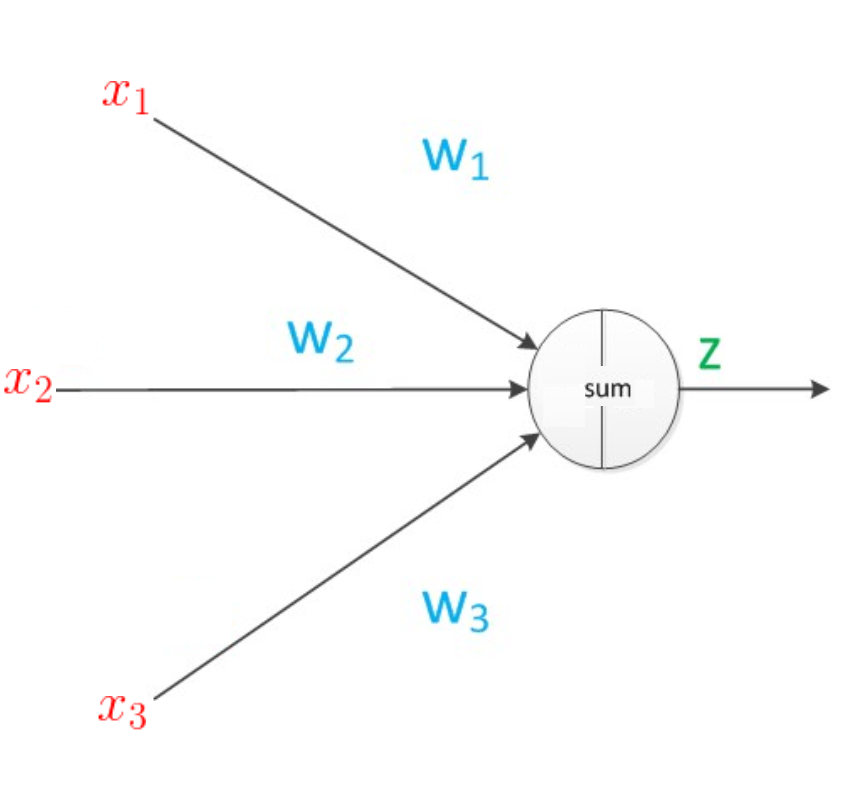
要求神经网络的输出:
是一类
是另一类
可见,感知机就是单层的神经网络(这里以连接线的层数表示网络层数)
逻辑回归
逻辑回归也是单层神经网络,证明如下:
构建神经网络——
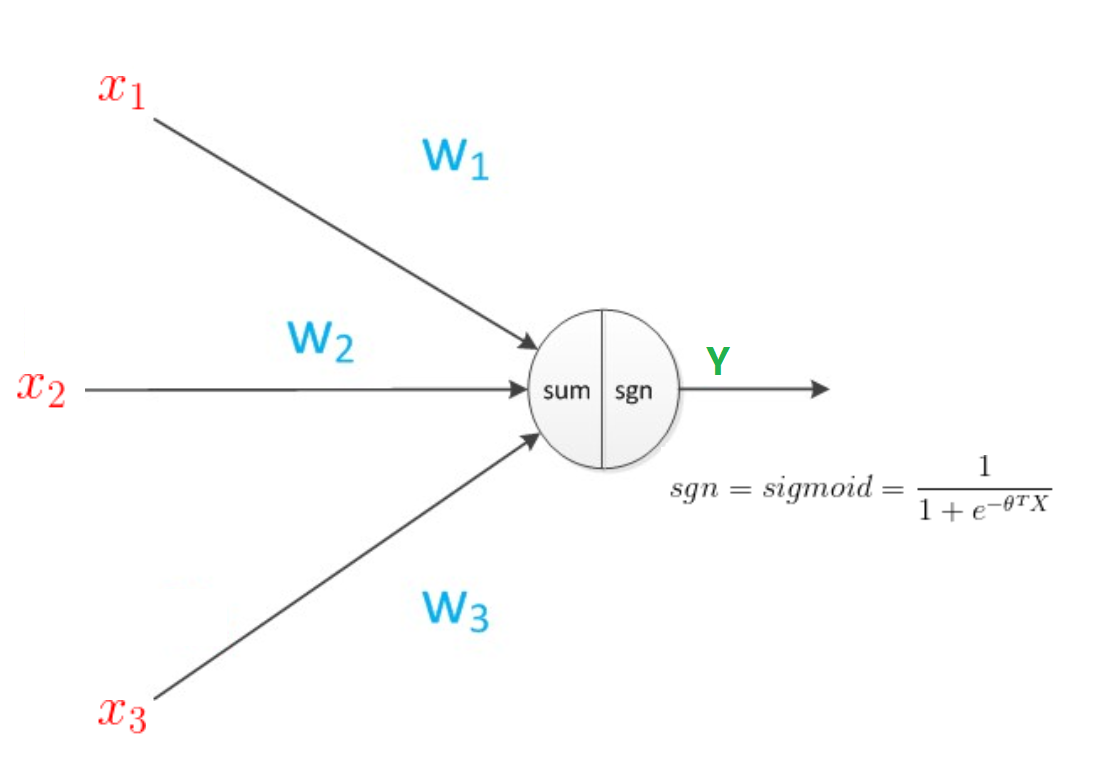
则:
证毕。
神经网络的矩阵表示
通过矩阵相乘可以表示一个神经网络,以单层为例:
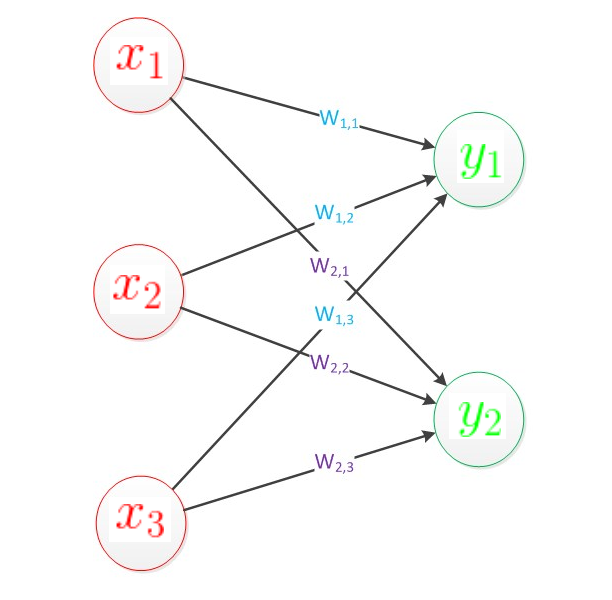
上面的过程可以表示为:
或者取转置,为:
如果是多层神经网络,则为多个权重矩阵连乘
神经网络的偏置
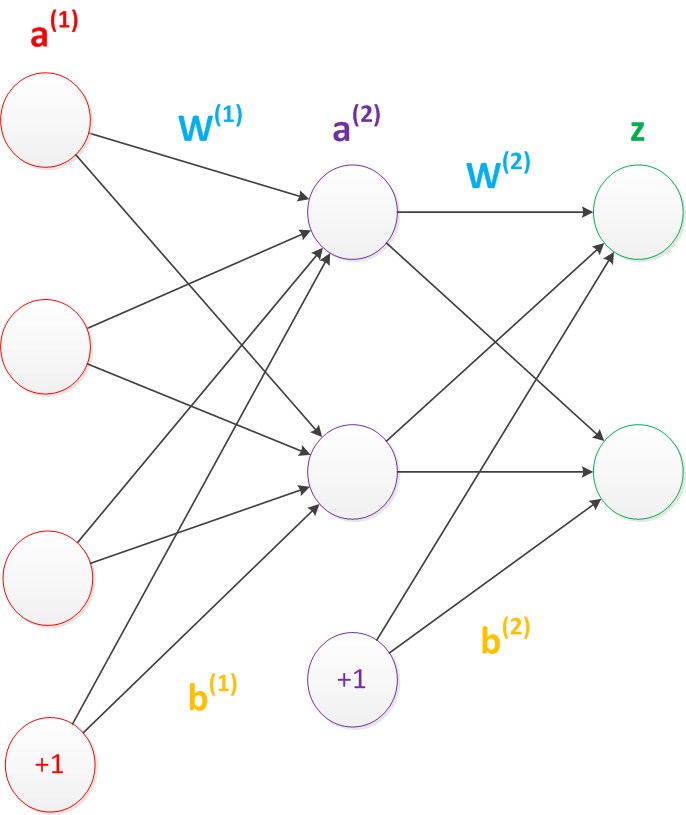
偏置可以看作对除了输出层的每一层(输入层和隐藏层)加入一个平行的常数输入:1
它的权重为 (假设局部输出为m个)
那么对于上面的例子来说,可以用矩阵表示为:
神经网络的训练
训练网络就是在结构已经确定的情况下,训练权重和偏置。
首先我们从目标函数入手。输出值作为预测值,那么预测值和label值是有差别的,我们用常见的均方误差来表示这个差别:
其中为预测值,它可以通过权重来表示,
为第i个样本的label值。
容易想到,我们只要将e对相应权重或偏置求偏导,然后通过梯度下降法,使得e最小,就能找到该权重或偏置的最优值。我们来推导求偏导公式,为便于理解,考虑下面的网络(假设没有激活函数或者理解激活函数为原样输出):
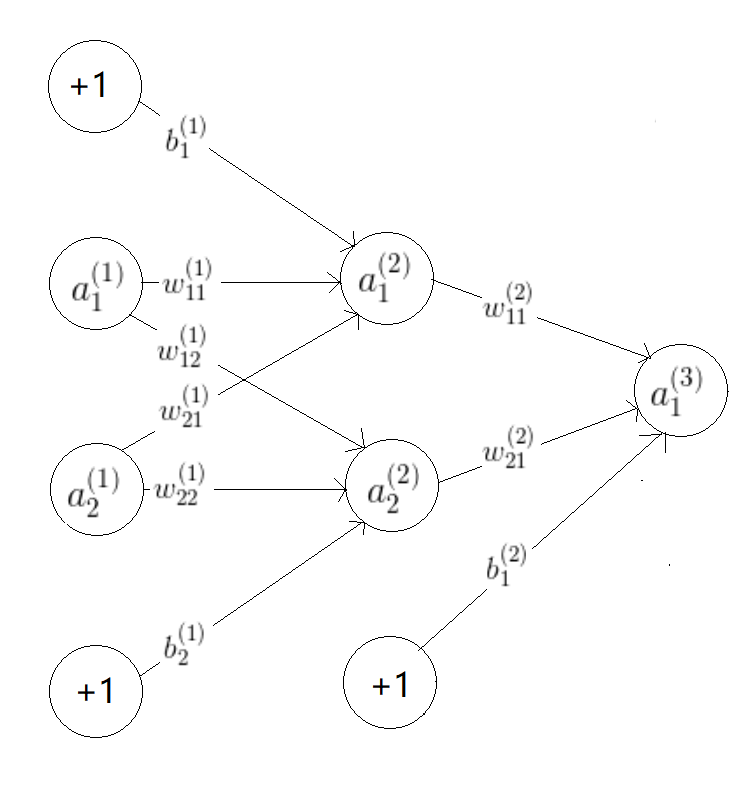
比如我们考虑第一层权重对e的影响,采用链式求导:
考虑第二层权重:
第一层偏置:
第二层偏置:
上面任何一个公式都可以得到一个关于被求偏导变量的梯度表达式,只要采用梯度下降就能得到迭代公式,就可以开始训练了!
不过,在梯度下降前,有没有更优化的方法呢? 乍一看,各种权重和偏置的计算当中有一些共有的部分,你能找出准确的代数关系以方便我们不重复计算共有部分吗?如果你能找出来,那么你可能发明了Back Propgation反向传播算法:
首先,我们人为定义一种“误差”。这种“误差”就是总损失e对各层各神经元的偏导。
比如第1,2,3层第1个神经元的误差分别为:
可以推得误差的反向迭代公式:
①
再代入上面的权重的偏导:
推得权重的反向迭代公式:
②
同理对于偏置的偏导:
推得偏置的反向迭代公式:
③
通过上面的迭代公式,我们可以更快速地计算出偏导数。求出来之后?跟之前一样,采用梯度下降就好了:
以上。