Random Forest 随机森林,它的名字包含了两个信息 1)是用很多决策树组成的森林;2)是采用随机的特征选取和样本选取方法。
它的名字没有包含的信息或许更加重要:Bagging方法
Bagging
Bagging 常常和Boosting放一起讨论,他们作为Ensemble Learning集成学习的两种方法而存在。
Bagging指的是有放回的方法,在随机森林的构建上就是:每棵决策树用的是同样的样本集(当然,每次真正选择的参与建树的样本可以不同,以减轻over-fitting的可能)。也就是说这些样本在用来构建一棵树之后,又放回去了,再来构建后面的树。所以与Boosting加法性质不同,Bagging构建出来的每棵树之间是平行关系。那么最后决策采用投票方式,就比较容易理解了。
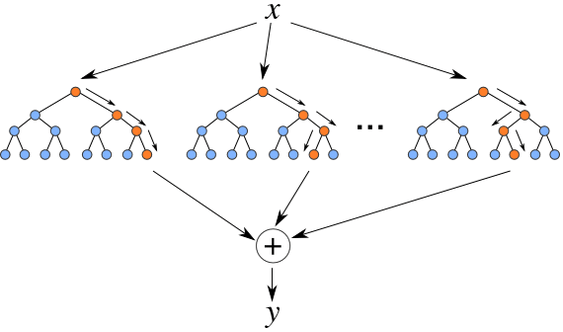
每棵树的生成
如果训练集为N,特征数为M,则一棵树的生成过程如下:
1)随机抽取个样本
2)随机抽取个特征
3)使用子集,构建决策树(ID3,C4.5,CART)。以CART分类树为例,创建任何一棵树的过程:
3.1)选择m个特征分裂里基尼指数最高的那个,开始二叉(CART分类树使用的是二叉)分裂
3.2)如果到了叶子节点,则该分支停止,否则继续选择基尼指数最高的特征继续分裂
3.3)如果分裂用尽了所有特征,而还没到叶子节点(通常是因为最初m个随机特征的抽取的时候,某些决定性特征没有被选中导致的),则以某个类别的样本数量最多的为强制叶子节点
4)创建N棵树(N为停止条件,试情况而定)之后,停止建树,采用投票机制选择得票最高的那个类别
以上为训练过程,预测过程就是用待预测数据走通上述过程,得到预测结果投票最高的那个。
随机森林举例
以CART里讲过的数据集为例,预测是否放贷:
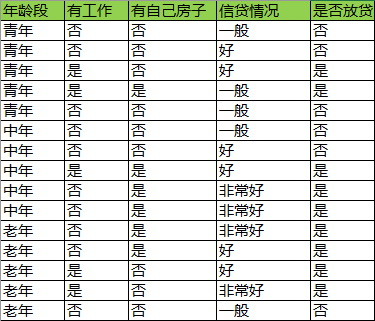
1)随机抽取9个样本
2)随机抽取三个特征:是否青年,是否有工作,是否有自己房子
样本,特征选取如下:
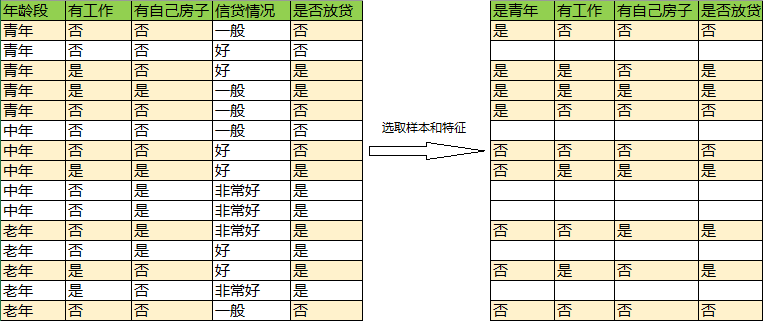
以分别表示青年,有工作,有房子三个特征,则Gini指数分别为:
其中“有工作”与否的分裂点基尼指数最小,所以以它为分裂点进行分裂
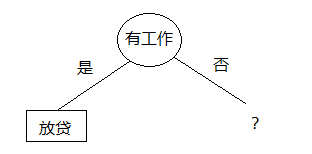
接下来计算没工作情况下的分支,数据为:
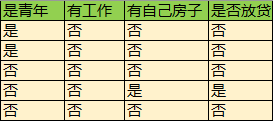
计算青年,有房子两个特征的基尼指数:
“有房子”与否的基尼指数最小,选择它。有:
第1棵树: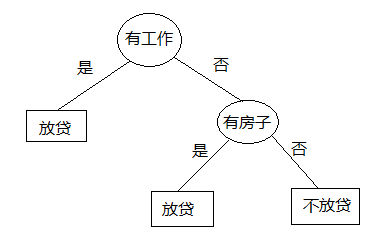
第一棵树建树完毕。
3)重复 1),2)建更多的树(不妨设总棵数为4):
第2棵树: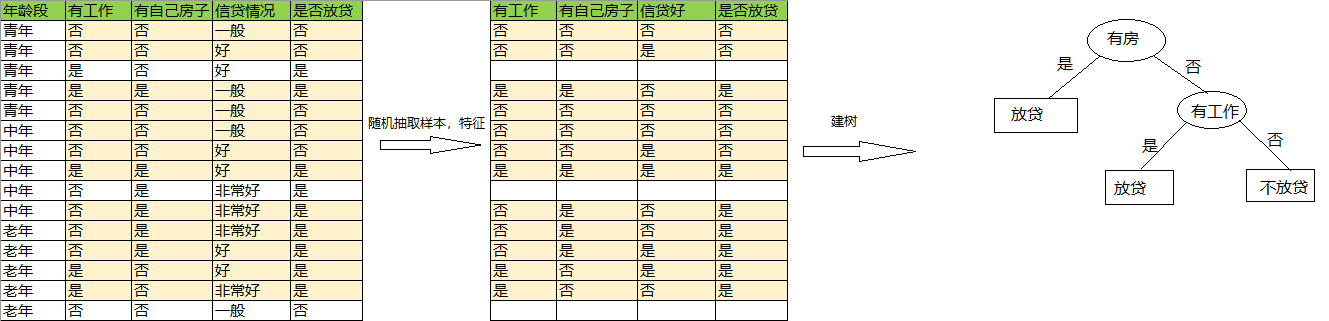
第3棵树: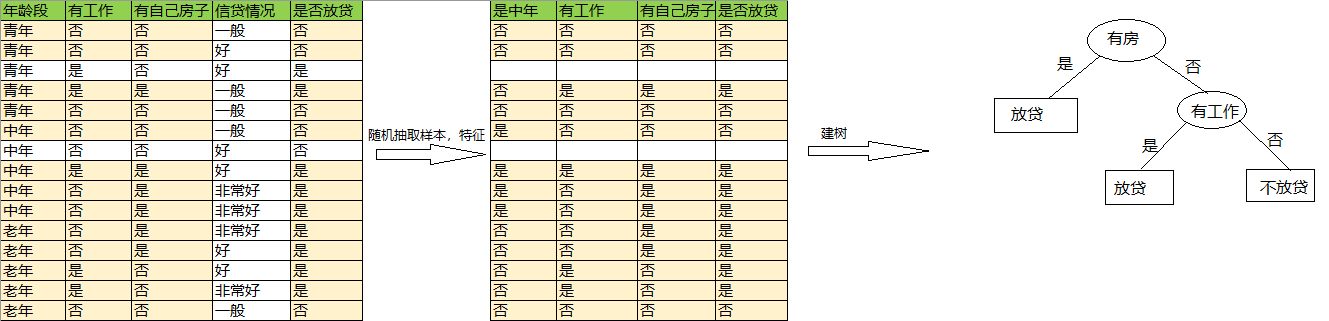
第4棵树: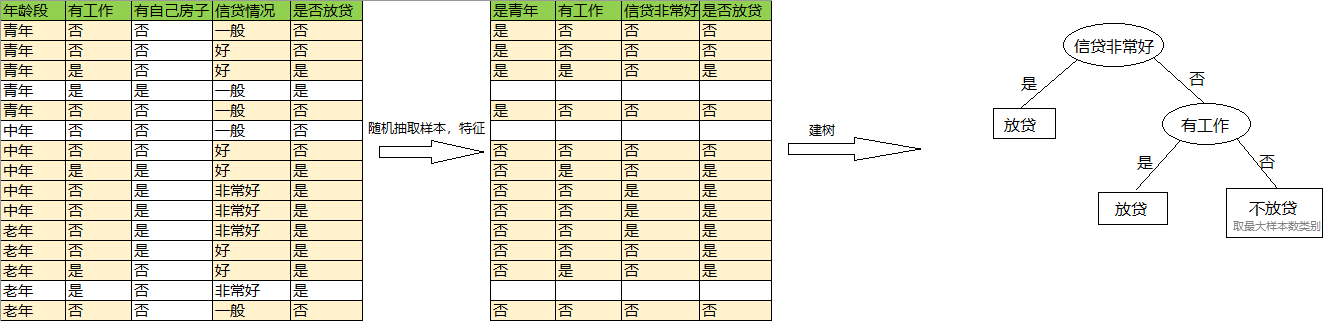
4)现在有一个人的特征是:中年,没工作,没房子,信贷非常好。 预测是否向Ta放贷?
第1棵树:不放贷
第2棵树:不放贷
第3棵树:不放贷
第4棵树:放贷
通过投票,放贷票数最多。所以最后预测结果为:不放贷。
以上。