eXtreme Gradient Boosting简称XGBoost,不算一种全新的算法,而是GBDT的一种高效的实现,它的repo在这里
XGBoost在GBDT基础上进行了很多抽象和优化,以至于乍一看不像同一个算法了。接下来解释XGBoost的原理
XGBoost原理推导
首先它继承的是GBDT的Boosting思想,也就是生成多颗树,每棵树都有对某个样本的预测,用加法模型将多颗树对该样本的预测结果相加,就是该样本的最终预测结果。而损失函数和GBDT一样,都是对所有样本预测值和label值偏差的求和,这个偏差可以是均方误差也可以是别的误差。不同的是XGBoost抽象出了损失函数并且加上了惩罚项:
其中为GBDT的损失函数,是样本偏差之和,
为样本数,
为偏差函数,比如均方误差,
为样本的label值,
为预测值。
为惩罚项,
为树的总棵树,
为所有树的叶子总个数,
为第j个叶子的值,这里用的是它的二范数。
是乘数因子。
可以看出惩罚项惩罚的是总叶子的个数,相当于也惩罚了树的颗数。以此降低过拟合风险。
接下来把注意力放到住损失函数上来。现在想象我们已经生成到了第t一棵树,我们当然希望,这第t颗树的生成使得总损失减少了,不然就没必要生成第t棵树了。
设第t棵树的预测对样本的预测函数为
,那么样本的最终预测值是所有树的预测值之和,也是前t-1棵树的最终预测值加当前树的单独预测值:
代入到损失函数中,得到t颗数总损失为:
接下来巧妙的来了:将函数在点
处按泰勒二次展开,并去掉常数项:
其中为偏差函数
在点
处的一阶导数,
为偏差函数
在点
处的二阶导数
我们回顾一下GBDT的梯度,它只用到了对偏差函数一阶导数。所以说这里,使用二阶导数是XGBoost的一个优化,这样使得它能够使用任何损失函数,比如最小二乘函数(参考),以此提高扩展性。
注意,上式之所以可以去掉常数项,是因为损失函数作为目标函数,进行最小化的过程中,常数项不影响求导结果,所以不影响目标参数的求解结果。被去掉常数项的损失函数的第一项求和部分可以理解为第t棵树里每个样本的损失之和。
下面,欲将以上目标函数写成按照叶子节点求和的形式。首先设,表示是总叶子数中第
个叶子的值,而
是落入第t棵树的。在一棵树里,n个总样本中,总是多个样本为一组,落入每个叶子中,并共享同一个值,每棵树都如此,只是每棵树的样本分组方式不一样。同时,第一项求和部分为第t棵树里每个样本的损失之和。考虑上述形式,将目标函数改写为:
其中表示第j个叶子里落入的那组样本的下标,它们是共享同一个值
的。 令
,则:
要求的是,所以对它求偏导为0,得:
求解得:
至此我们可以通过第t-1棵树的导数,来求各叶子的数值,包括第t棵树的叶子的值。
同时我们也可以得到目标函数的值,在节点分裂效果评估中会用到:
图示计算样例:
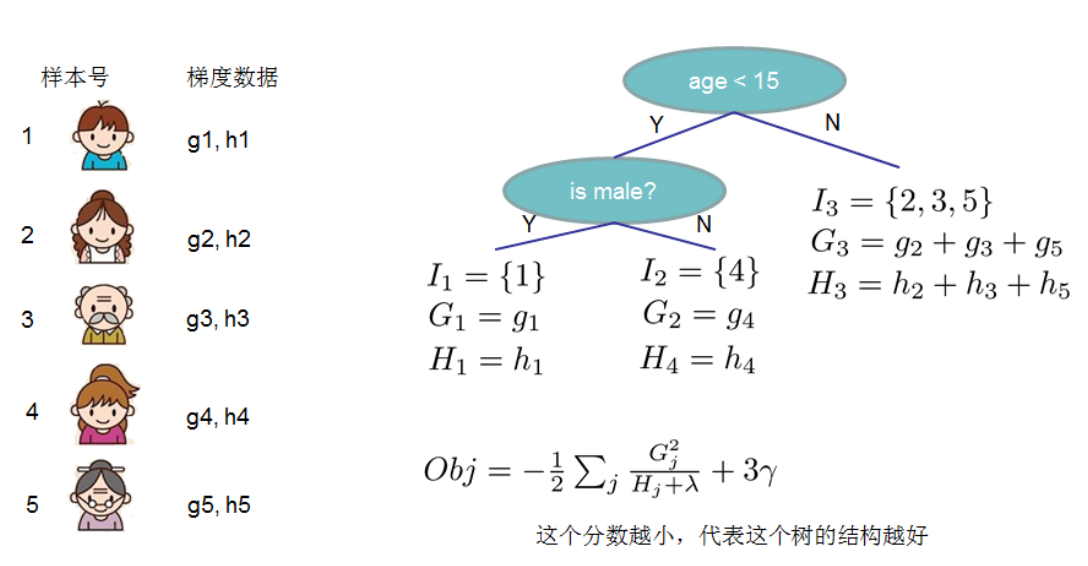
XGBoost的节点分裂
上一节只是基于树结构确定的情况下的叶子值求解算法,然而作为前提,树的特征分裂方法,还没有被讨论到。这一节就来讨论它。
XGBoost采用的方法是遍历所有特征的分裂点。如何评价分裂效果?使用上述的目标函数。只要逐一计算每种分裂方法下上述的目标函数的值,越小的分裂效果越好。当然不能无限制分裂,为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂:
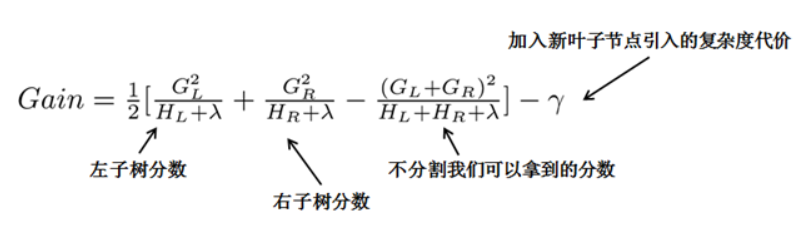
虽然需要贪心地计算很多遍分裂,但是好在特征的分裂是能够并行的
XGBoost的其它优化
时刻记住XGBoost是重在实现,它是个工具,提供了很多优化方式,在编程上,可以使用也可以不使用。
如针对稀疏数据的算法(缺失值处理):当样本的第i个特征值缺失时,无法利用该特征进行划分时,XGBoost的想法是将该样本分别划分到左结点和右结点,然后计算其增益,哪个大就划分到哪边。
如防止过拟合的Shrinkage方法:在每次迭代中对树的每个叶子值乘上一个缩减权重η,减小该树的比重,让后面的树有优化的空间。
又如防止过拟合的Column Subsampling方法:类似于随机森林,选取部分特征建树。可分为两种:1)按层随机采样,在对同一层内每个结点分裂之前,先随机选择一部分特征,然后只需要遍历这部分的特征,来确定最优的分割点;2)随机选择特征,则建树前随机选择一部分特征然后分裂就只遍历这些特征。一般情况下前者效果更好。
还有其它优化方式,不逐一讲解了:交叉验证,early stop,支持设置样本权重,支持并行化等。