HMM的定义

HMM即Hidden Markov Model，隐马尔可夫模型，是用来描述这样一种过程：有两类数据，一类是可以观测到的，为观测序列，一类是观测不到的，为隐藏状态序列，简称状态序列。比如知道一个人过去三天的活动序列是“逛街->运动->在家”，而想知道过去三天的天气序列是“晴->多云->雨”还是“多云->晴->雨”还是其它。这种情况我们可以构建HMM：将这个人的活动看做观测序列，天气看做隐藏状态序列，进而求各种状态序列的概率。当然也可以反过来知道状态序列，求这个人的某种活动序列的概率。再比如在语音识别中就利用了HMM，认为语音为观测序列，它背后的文字为状态序列。

在数学上表示HMM为：

初始状态矩阵： $\Pi=\begin{pmatrix} I_1\\ I_2\\ ...\\ I_n \end{pmatrix}$

状态转移矩阵： $A=\begin{bmatrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ & & ... & \\ a_{n1} & a_{n2} & ... & a_{nn} \end{bmatrix}$

观测矩阵（或混淆矩阵）： $B=\begin{bmatrix} b_{11} & b_{12} & ... & b_{1m} \\ b_{21} & b_{22} & ... & b_{2m} \\ & & ... & \\ b_{n1} & b_{n2} & ... & b_{nm} \end{bmatrix}$

HMM的例子

通过一个例子解释它们的含义：

一个包含三个状态的天气系统（晴天、多云、雨天）中，可以观察到4个等级的海藻湿润情况（干、稍干、潮湿、湿润）。

初始化的的时候，晴，多云，雨出现的概率分别为0.5,0.15,0.35，则初始状态矩阵为:

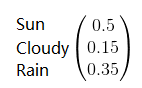
对于隐状态序列：上个状态为晴天的情况下，转移到当前状态也为晴天的概率为0.5，转移到多云的概率为0.375，转移到雨的概率为0.125（加起来为1）；上个状态为多云的情况下，转移到当期为晴天的概率为0.25，转移到多云的概率为0.125，转移到雨的概率为0.625….所以状态转移矩阵为：

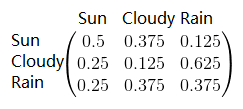
对于观测序列：若当前状态为晴，观测到海藻为干的概率是0.60，观测到海藻为稍干的概率是0.20 …;若当前状态为多云，观测到海藻为干的概率是0.25，观测到海藻为稍干的概率是0.25 ….所以观测矩阵为：

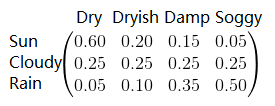
HMM的三个问题

HMM被使用来解决三个方面的问题：

1）评估观测序列。给定观测序列和多个确定的模型（ $\Pi ,A,B$ ）,求这个观测序列在每个模型出现的概率，以判断现在使用的是什么模型。比如上面的天气-海藻湿度问题，我们可能有春季模型，夏季模型，秋季模型，冬季模型。分别计算不同模型下当前观测序列出现的概率，选概率最大的，就能知道现在是什么季节。这里面会用到前向算法或者后向算法

2）解码。给定观测序列和模型（ $\Pi ,A,B$ ）,求最可能出现的状态序列，比如语音识别，文本分词。会用到维特比算法

3）学习。给定观测序列和模型的参数估计值（而非实际值），求模型的实际值。会用前向-后向算法，也称作Baum-Welch算法

我们分别讲这三个问题的解决方法。

评估观测序列(一)：前向算法

依然考虑上面的天气-海藻的例子。

现在我们观测到连续三天的海藻状态是：dry-damp-soggy

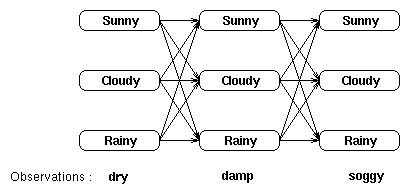
问在当前的模型下，出现这种观测序列的概率是多少？

如果是暴力计算的话，我们可以穷举 $3^3=27$ 条路径的概率，然后把它们的概率相加，得到我们要的结果，比如其中的一条路径的概率计算如下：

sunny(dry)->cloudy(damp)->rainy(soggy): P[sunny(dry)->cloudy(damp)->rainy(soggy)]=[P(sunny)P(dry|sunny)]*[P(sunny->cloudy)P(damp|cloudy)]*[P(cloudy->rainy)P(soggy|rainy)]

代入数值计算： $(0.5*0.6)*(0.375*0.25)*(0.625*0.5)=0.0088$

我们可以建立一个递归模型，来替代暴力计算。

假设一个序列从1开始到T时刻结束：

输入：HMM模型 $\lambda=(\Pi ,A,B)$ ，观测序列 $O=(o_1,o_2,...,o_{T})$

输出：观测序列概率 $P(O|\lambda)$

1) 计算时刻1的各个隐藏状态前向概率：

$\alpha_1(i)=\pi_ib_i(o_1),\ \ i=1,2,...n$

$\pi$ 为初始隐状态的概率，i为隐状态的序号， $b_i(o)$ 来自混沌矩阵，为第i个隐状态条件下观测到o的概率

2) 递推时刻2,3,…T时刻的前向概率：

$\alpha_{t+1}(i)=b_i(o_{t+1})[\sum_{j=1}^{n}\alpha_t(j)a_{ji}],\ \ \ i=1,2,...n$

$b_i(o_{t+1})$ 来自混沌矩阵，为t+1时刻第i个隐状态下观测到的 $o_{t+1}$ 的概率； $a_{ji}$ 来自隐状态转移矩阵，为第j个隐状态到第i个隐状态的转换概率

3) 计算最终结果：

$P(O|\lambda)=\sum_{i=1}^{n}\alpha_T(i)$

意思是最终结果的输出为最后一个时刻T的局部概率值和。

以上步骤就是前向算法。为了便于理解递归关系，选取t+1时刻对cloudy状态计算局部概率的图：

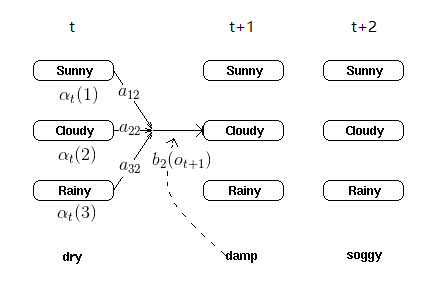
在实际应用中，我们用不同的模型（如春、夏、秋、冬模型）来算出不同的最终结果概率，比较哪个最大（最大似然思想），则是我们要求的季节。

评估观测序列(二)：后向算法

有了前向算法的基础，理解后向算法只要把状态序列的走向逆向就可以:

输入：HMM模型 $\lambda=(\Pi ,A,B)$ ，观测序列 $O=(o_1,o_2,...,o_{T})$

输出：观测序列概率 $P(O|\lambda)$

1) 初始化时刻T的各个隐藏状态后向概率：

$\beta_T(i)=1,\ \ \ i=1,2,...n$

全部初始化为1

2) 递推时刻T−1,T−2,…1时刻的后向概率：

$\beta_t(i)= \sum_{j=1}^{n}\alpha_{ij}b_j(o_{t+1})\beta_{t+1}(j),\ \ \ i=1,2,...N$

3) 计算最终结果：

$P(O|\lambda)=\sum_{i=1}^{n}\pi_ib_i(o_1)\beta_1(i)$

图示理解:

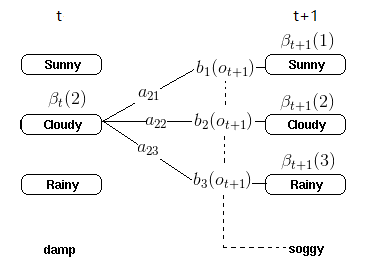
解码：维特比算法

考虑这样一个问题：给出观测序列和模型，找出最可能的隐状态序列。

如果是暴力计算的话，我们可以穷举 $3^3=27$ 条可以导致改观测序列的隐状态序列路径，找出哪条路径能最大概率地导致该观测序列，也就是我们要找的路径。

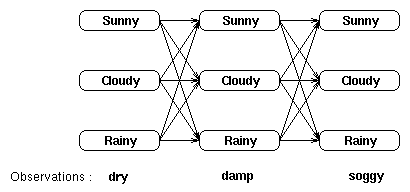
比如其中的一条路径的概率计算如下:

sunny(dry)->cloudy(damp)->rainy(soggy): P[sunny(dry)->cloudy(damp)->rainy(soggy)]=[P(sunny)P(dry|sunny)]*[P(sunny->cloudy)P(damp|cloudy)]*[P(cloudy->rainy)P(soggy|rainy)]

代入数值计算： $(0.5*0.6)*(0.375*0.25)*(0.625*0.5)=0.0088$

可以发现单独计算一条路径跟评估观测序列里面的做法是一样的。不一样的在后面我们需要比较各条路径，而评估观测序列是需要把各条路径概率相加。

不用暴力计算，用维特比算法，流程如下：

输入：HMM模型 $\lambda=(A,B,\Pi)$ ，观测序列 $O=(o_1,o_2,...,o_T)$
输出：最有可能的隐藏状态序列 $I^*=\{i^*_1,i^*_2,...,i^*_T\}$

1）当t=1时，初始化局部状态：

$\delta _1(i)=\pi_ib_i(o_1),\ \ i=1,2...n$

$\psi _1(i)=0,\ \ i=1,2...n$

其中i表示第i个隐状态，
$\pi_i$ 为第i个隐状态的初始概率， $b_i(o_1)$ 表示第i个隐状态下观测到 $o_1$ 的概率； $\psi _1(i)$ 为目前为止的最大概率路径

2) 进行动态规划递推时刻t=2,3,…T时刻的局部状态：
$\delta _t(i)=\underset{1\leq j\leq n}{max}[\delta_{t-1}(j)a_{ji}]b_i(0_t),\ \ i=1,2,...,n$

$\psi _t(i)=arg\ \underset{1\leq j\leq n}{max}[\delta _{t-1}(j)a_{ji}],\ \ i=1,2...,n$

其中 $\delta _t(i)$ 表示t时刻的能观测结果的隐状态序列组合的最大概率； $\underset{1\leq j\leq n}{max}[\delta_{t-1}(j)a_{ji}]$ 表示到t-1时间为止的最大概率的路径的概率； $b_i(0_t)$ 表示第i个隐状态下观测到 $o_t$ 的概率； $\psi _1(i)$ 为目前为止的最大概率路径

3) 计算时刻T最大的δT(i),即为最可能隐藏状态序列出现的概率。计算时刻T最大的Ψt(i),即为时刻T最可能的隐藏状态。

$P^*=\underset{1\leq j\leq n}{max}\delta _T(i)$

$i^*_T=arg\ \underset{1\leq j\leq n}{max}[\delta _T(i)]$

4) 利用局部状态Ψ(i)开始回溯。对于t=T−1,T−2,…,1：

$i^*_t=\psi _{t+1}(i^*_{t+1})$

这表示，我们需要往后走一步，才能得到当前这个隐状态序号。最终得到最有可能的隐藏状态序列:

$I^*=\{i^*_1,i^*_2,...i^*_T\}$

通过图示理解上面的迭代过程：

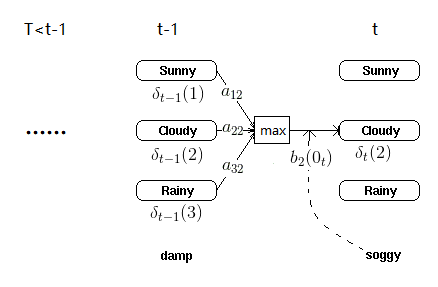
学习：Baum-Welch算法

学习的目标是求解未知的HMM的参数。

已知D个时刻为T的观测序列和对应的隐藏状态序列，即 ${(O_1,I_1),(O_2,I_2),...,(O_D,I_D)}$ 是已知的，此时我们可以用最大似然来求解模型参数。也就是说 $O_1$ 在 $I_1$ 的状态下被观测到，是因为“ $I_1$ 本身的初始状态”乘以“ $I_1$ 情况下 $O_1$ 被观测到的概率”的结果，是最大的。也就是说 $\pi_{I_1}*b_{I_1}(O_1)$ 比其它组合都大，最好的结果就是乘子的每一部分都是各自领域最大的：

1） $\pi_{I_1}$ 大于 $\pi_{I_2}$ 和 $\pi_{I_3}$ 等其它初始状态概率

2） $b_{I_1}(O_1)$ 大于 $b_{I_1}(O_2)$ 和 $b_{I_1}(O_3)$ ，…, 等其它观测概率

同理，在非初始情况下， $O_i$ 在 $I_i$ 的状态下被观测到，根据“乘子的每一部分都在各自领域最大”的推断，是因为从上一个隐状态 $I_{j}$ 转移到这一个 $I_i$ 的概率最大，同时观测到 $b_{I_i}(O_i)$ 的概率最大也就是:

3）在状态转移矩阵A的一行里面， $a_{ji}$ 比其它值 $a_{j1}$ ， $a_{j2}$ , …等都大

4）在观测矩阵B的一行里面， $b_{I_i}(O_i)$ 比其它 $b_{I_i}(O_2)$ ， $b_{I_i}(O_3)$ ，…等都大

以上，根据1）2）可以求初始矩阵，根据3）4）可以求状态转移矩阵A和观测矩阵B,当然可能不止一个解。

上面的例子很美好，是因为它同时告诉了我们隐状态的序列和观测序列。如果只告诉我们观测序列，而隐状态序列未知，怎么求HMM模型的参数呢？

首先，我们可以想到我们面临的状况很类似于EM算法的背景。在EM算法里面，我们在只知道试验结果而不知道隐含条件的情况下，能够通过反复猜想-估计得出目标概率。没错接下来要用的Baum-Welch算法实际上是基于EM算法，不过它提出的时间比EM算法早。Baum-Welch算法像EM算法一样，没有参数值，就猜出一个参数值，代入进去计算，不断反复，直至收敛到一个理想参数。

中间公式的推导就不给出了，直接给出Baum-Welch（鲍姆-韦尔奇）算法的流程。

输入： D个观测序列样本 $O=(o_1,o_2,...,o_{T})$

输出：HMM模型参数

1）随机初始化所有的 $\pi_i,a_{ij},b_j(k)$