EM 算法

EM算法原理

EM（Expectation Maximization）期望最大化。主要通过极大似然估计来实现隐含条件的概率估计。

通过实例来理解

简单实例

有两枚不规则的硬币，进行试验：先随机选一个硬币，然后抛掷5次，记录正面和反面的次数。这样的试验一共进行了5轮，我们知道的信息只有这5轮的结果为：

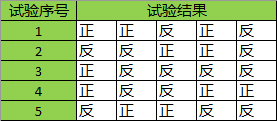
问：如何估计这两枚硬币的正面出现的概率？

这个例子里面的隐含条件是“随机选一个硬币”选中的是哪一个硬币。如果知道每次选中是哪一个硬币，那么通过频率我们可以很快算出每个硬币出现正面的概率。但是现在我们不知道它每次选中的是哪一个硬币。我们采用的方法是：

1）猜。

当然不是猜每次选中的是哪一个硬币，那只是个中间变量，最终是为了求正面概率，所以我们直接猜最终要求的每个硬币出现正面的概率。我们猜1号硬币的正面概率是0.2，2号硬币的正面概率是0.7

2）顺猜而为。

现在假设我们刚才的试验的前提是概率就是0.2和0.7，然后出现了上面试验的结果。为什么会偏偏出现这个结果，而不是另外的结果呢？我能看到这个结果，一定不是巧合，而是因为这个结果很容易出现，就算别人再来做一遍，也是有比较大可能会看到这个结果的（此为最大似然估计的思维）。所以来试试分析：

我们试一下如果每轮分别是选的1号硬币和2号硬币，出现本轮正反组合的概率是多少。比如第1轮，如果选的是1号硬币，那么它出现“正正反正反”的概率是0.00512，很难出现。如果选的是2号硬币，那么它出现“正正反正反”的概率是0.03087，相对更容易出现。现在的事实是，我们观测到“正正反正饭”这个结果了，所以我们估计于本轮选择的2号硬币。

据此算法，得出5轮下来对硬币选择的估计如下：

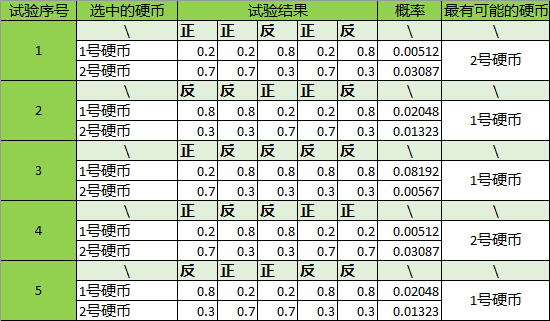
3）反算猜测值。

好，现在我们已经对每次选择的硬币是哪一个有了第一次的估计结果。现在我们基于这个硬币选择的方式，再来算一下每个硬币的证明出现的概率，看看它跟我们最开始猜的是否接近。

一共进行了25次抛掷：
1号硬币被抛掷了15次，有5次正面：通过频率算概率为
2号硬币被抛掷了10次，有5次正面：通过频率算概率为

相当于将我们猜的概率更新为0.33， 0.6

4）接下，使用更新后的概率猜测0.33和0.6继续进行上面的“顺才而为”和“反算猜测值”，并循环至收敛，就能得到最终的概率估计。

一定可以收敛吗？是的，不过这里不作证明了。

最终会收敛到：

1号硬币出现正面的概率：
2号硬币出现正面的概率：

进阶实例

上面的例子中，当进行到1号硬币和2号硬币的选择时，我们依照出现的容易程度选择了其一而完全抛弃了其二，这样对信息是由损失的。为了用上所有的信息，我们不轻易抛弃任何一个结果。这样我们可以使用期望来计算：

如第1轮中，1号硬币被选择的概率是0.00512，2号硬币被选择的概率是0.03087，它们二者归一化的比例是14%和86%.
计算方法：

也就是说，第一轮中5次里面任何1次：1号硬币的出现正的期望是0.14,2号硬币出现正的期望是0.86，它们加起来才是“1”次正；同理1号硬币的出现负的期望是0.14,2号硬币出现正的期望是0.86，它们加起来才是“1”次负

根据期望计算，如果只计算1号硬币，则它第一轮出现次正，次负

计算1号硬币的其它轮次的正负期望，并对2号硬币进行同样计算，得到统计表格如下：

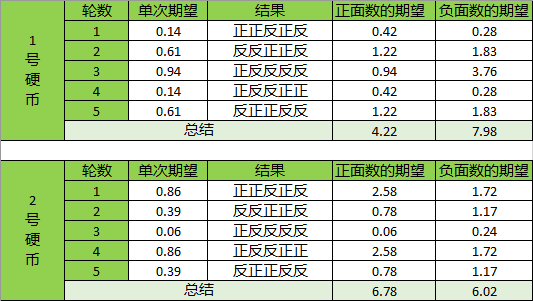
也就是说：

1号硬币总共4.22次正面，7.98次负面 => 出现正面的概率为

2号硬币总共6.78次正面，6.02次负面 => 出现正面的概率为

可见相比“抛弃”的做法，我们更充分利用信息，能更快接近真实概率

以上。