问题的提出
我们考虑一个股票推荐的数据集,它每行是一个样本。每个样本有四个特征,推荐结果只有“推荐”与“不推荐”两类:
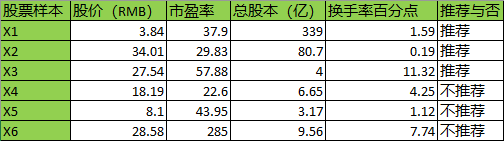
基于以上的数据集,我们训练一个分类器。首先将推荐结果量化表示:1表示推荐,0表示不推荐。
那么对前3个样本中的任何一个
,我们希望分类器应该能将它分类到1,而对后3个样本
中的任何一个
,我们希望分类器应该能将它分类到0。
从这里开始,假如用线性回归的思维,我们可以训练出一个这样的模型:,当
时,归到1类;当
时,归到0类。 这样分类精度会很低。
我们这里要使用的是逻辑回归,也就是Logistic Regression。注意它不是回归,而它是一种分类算法。
逻辑回归
概率模型
让我们的分类器输出概率,并设定决策方式为:分类到概率更大的类别,即:对前3个样本中的任何一个
,分类器应该将它分类到1的概率大于0.5; 对后3个样本
中的任何一个
,分类器将它分类到0的概率大于0.5。用数学表示就是:
以上式子中Y是类别,为模型的参数,它可能是标量,可能是向量,取决于模型是什么。那模型究竟是什么呢?我们可以合理创造它——
我们看到这里求的是概率,所以模型应该是取值为的函数,而我们正好有一个著名的函数Sigmoid,其取值正是为
:
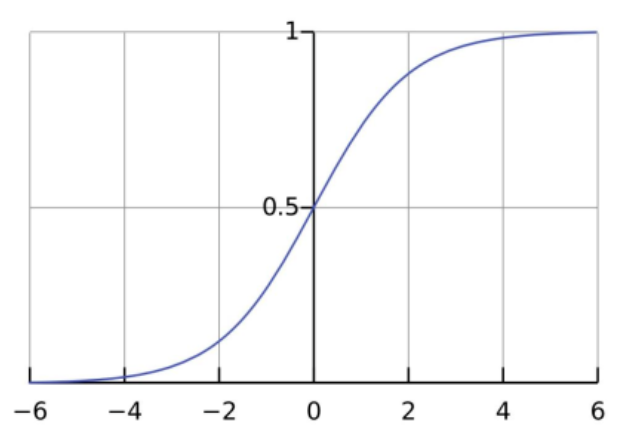
函数表达式:
所以我们想到将线性特征嵌入Sigmoid中,设:
①
BTW,此模型下,参数
这个时候,可能有人问,为什么一定是这样的线性组合?当然不一定,你可以使用更复杂的组合。然而这里的线性组合是简单的且被证明work的,为什么不用呢?
回到我们的推导。Y=0的概率与Y=1的概率互补,既然Y=1的概率模型已经出来了,那么轻松得到:
②
这里我们可以do a trick,将①和②合并(之后会用到):
③
损失函数
现在我们已经得到了概率模型。此时我们可以通过极大似然的思维方式得到损失函数,即既然已经分类出来了,那么就不满足概率仅仅大于0.5,而是让分到这个类的概率尽可能大,如果我们的训练样本数为m个,那么我们希望m个概率的乘积尽可能大。所以似然函数是,我们需要最大化它。取负号就是最小化它,于是它损失函数就是损失函数:
损失函数求导
为了方便求导,设:
上两式求分别对求导:
注:这里对是因为
是一个向量,我们最终是要求出该向量的所有维度的值。
将代入损失函数:
好了,准备就绪,开始对损失函数求导:
至此,我们得到参数更新的迭代公式为:
接下来怎么办?——更新参数,训练分类器。训练过程由软件完成,这里就不手动推导了。