在介绍朴素贝叶斯之前,先简要回顾一下贝叶斯
贝叶斯定理
定理表达式:
它描述的是,我们对A事件有一个先验的概率判断,然后B事件发生了,它影响了我们对A事件的认识,影响因子为
,那么调整后的A的概率为
。当然我们可以把更新后的A事件的概率当做新的先验概率,然后继续使用贝叶斯定理,通过新事件B的加入,再次更新我们对A的认识。它的伟大在于,描述了人类大脑的思维方式,即通过新信息的加入,不断改变对一个事物的认识。在机器学习里有着广泛应用,因为它描述正是从初始值不断学习,逐渐趋近真相的过程
朴素贝叶斯 V.S. 贝叶斯
朴素贝叶斯假设的是条件之间互相独立,网路得以简化。比如:
1)已知行业和工时的条件下,计算收入>Z的概率 -> 贝叶斯
2)已知行业和姓氏的条件下,计算收入>Z的概率 -> 朴素贝叶斯
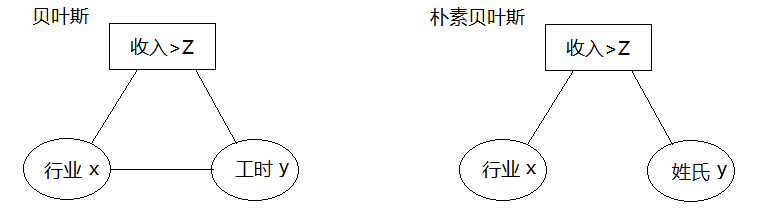
上面是基于事实情况的,但是在实践中,为了使用朴素贝叶斯进行机器学习,我们常常假设条件互相独立(即使它们不独立),这样进行学习的结果是有精度损失的,当然我们使用它就是因为能够承受该损失。在条件之间的相关性非常大的时候,使用朴素贝叶斯法会使得精度大打折扣,那时应该直接使用贝叶斯法或者别的方法
朴素贝叶斯分类器
分类操作中我们往往给定几个特征,要求将它归类到某一类。使用朴素贝叶斯作为分类器,就是把给定的特征和各个类作为发生的事件,求解在给定特征发生的情况下各个类发生的概率,并且将概率最大的那个类作为结果输出。
假设我们有下面的数据:在A,B,C,D四种特征的组合下,归类为PASS或FAIL——
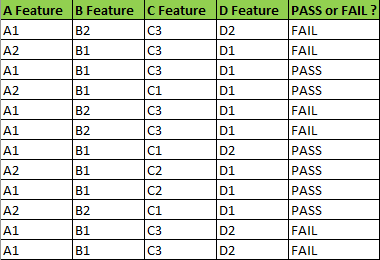
基于以上数据,现在有一个数据含有A2,B2,C3,D2四种特征,问该数据应该归类到PASS还是FAIL?
为了求解,我们首先将问题转换为贝叶斯的表达:
1) A2,B2,C3,D2四个事件都发生了,那么结果为PASS发生的概率是多少,即求?
2) A2,B2,C3,D2四个事件都发生了,那么结果为FAIL发生的概率是多少,即求?
3) 以上哪个概率更大?
求解1)
①
利用朴素贝叶斯的假设条件:A,B,C,D各个特征独立,有:
②
③
将②和③代入①中,得:
求解2)
④
利用朴素贝叶斯的假设条件:A,B,C,D各个特征独立,有:
⑤
⑥
将④和⑤代入⑥中,得:
求解3)
显而易见结果为FAIL的概率更大,所以该朴素贝叶斯分类器对A2,B2,C3,D2四种特征组合下的数据的分类结果是:FAIL类
以上。