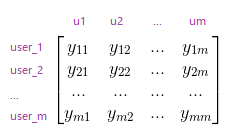
我们有一个样本集:
我们不妨把它当做一个m个用户对n个物品评分的矩阵。为了PCA计算方便,就把它当做一个已经去中心化的数据矩阵。
SVD的矩阵乘转置<=>PCA的协方差矩阵
我们先作一小步SVD分解:
按照SVD分解的方法,我们要获得中的U,需要对
进行特征值分解。
先来看看长什么样子:
看着很眼熟?好,我们再来做一小步PCA:
按照PCA的方法,假设我们以行向量(用户向量)为目标数据,item为维度,要对item数量进行降维,那么我们首先要计算已经去中心化的A的协方差矩阵:
去掉常数项,这不就是嘛!
至此,得:SVD中的就是PCA中以A的列为维度的协方差
同理,得:SVD中的就是PCA中以A的行为维度的协方差
SVD的奇异矩阵<=>PCA的特征向量
我们继续SVD,也就是求的特征向量
来表示原矩阵:
同时我们也继续PCA,也就是求协方差矩阵的特征向量并以它们为新的主元,写出新主元下的矩阵(即
):
当然, SVD中通过求得的右奇异矩阵
,与PCA中以行为维度的协方差求得特征向量也有上述的对应关系
所以在实际运算中,我们可以通过求SVD来求解PCA,也可以通过PCA来求解SVD。事实上很多运算库如scikit-learn的PCA算法实现就是用的SVD方法。
SVD的双向降维<=>PCA的单向降维
基于上面的求解结果,我们来进行最后的降维操作。这里以左奇异矩阵为例,右奇异矩阵请自行补脑。
使用SVD降维到k维时,会把左奇异矩阵截取(同时也会截取奇异值矩阵和右奇异矩阵,但是这里我们只关心左奇异矩阵)到前k个列向量:
使用PCA降维到k维时,会选择特征矩阵的前k个维度来表示原数据: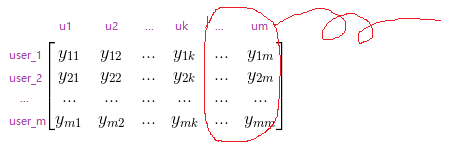
由此,我们可以认为,SVD对左奇异矩阵的降维就是对user向量的降维,而对右奇异矩阵的降维,就是对item向量的降维。SVD分解在推荐系统里基于这个结论才能顺利进行下去
总结
1) SVD可以做双向降维,它将行向量(user)和列向量(item)都进行降维了; PCA只能做单向降维,需要一开始指定维度是列(目标是user向量)还是行(目标是item向量),再进行降维操作
2) SVD相当于在行向量和列向量分别进行了PCA,并保存新主元到左奇异矩阵和右奇异矩阵中